A hybrid grid-point statistical interpolation-ensemble transform Kalman filter (GSI-ETKF) data assimilation system for the Weather Research and Forecasting (WRF) model was developed and applied to typhoon track forecast with simulated dropsonde observations. This hybrid system showed significantly improved results with respect to tropical cyclone track forecast compared to the standard GSI system in the case of Muifa in 2011. Further analyses revealed that the flow-dependent ensemble covariance was the major contributor to the better performance of the GSI-ETKF system than the standard GSI system; the GSI-ETKF system was found to be potentially able to adjust the position of the typhoon vortex systematically and better update the environmental field.
Although accuracy of tropical cyclone (TC) track forecast is improving, it is still facing many challenges. One of them is how to reduce the error in the initial condition that is usually produced by a data assimilation (DA) system. For most operational applications, a three-dimensional variational (3DVAR) DA scheme is employed to obtain initial states in which observation information is spread to model grid points to correct the background (forecast) field with the assumption of a static, homogeneous, and isotropic background error covariance. However, generally these assumptions cannot be used for applications related to TCs due to their strong vortical and nongeostrophic motions ( Hamill and Snyder, 2000). As a consequence, different techniques have been developed, for example, insertion of a “bogussed” vortex into the analysis field (e. g. , Kurihara et al. , 1995) or repositioning of TCs to the observed location during DA (e. g. , Liu et al. , 2000). While such techniques have been shown to improve TC track forecast, they are limited by their own assumptions.
Recent studies have suggested a that hybrid ensemble-3DVAR DA scheme can be an attractive approach for the initial estimation of a TC state due to its flow-dependent error statistics, which leads to a better representation of the strong spatial variability near TCs ( Li et al. , 2012; Wang, 2011). Wang (2011) showed that the flow-dependent error statistics of hybrid schemes could correct the TC structure and position without the help of extra vortex techniques described above.
Compared to the traditional ensemble Kalman filter (EnKF), application of the hybrid approach has the following advantages:(1) The hybrid system can be built upon an existing operational variational framework and thus ensemble information can be incorporated into the system relatively easily.
(2) Unlike a standalone EnKF, the hybrid system requires much less ensemble members and, as a result, is less vulnerable to model errors ( Wang et al. , 2007, Wang et al.2008a, Wang et al.2008b).
In this study, to evaluate the impact of a hybrid DA system on the TC track analyses and forecasts, a hybrid grid-point statistical interpolation-ensemble transform Kalman filter (GSI-ETKF) system was developed and applied to the track forecast of typhoon Muifa case in 2011. Specifically, we built the hybrid GSI-ETKF system for the Weather Research and Forecasting (WRF) model based on the existing grid-point statistical interpolation system (GSI, an operational 3DVAR system used in the National Centers for Environmental Prediction (NCEP); Wu et al. , 2002; Kleist et al. , 2009) and an ETKF system ( Wang and Bishop, 2003; Wang et al. , 2004, Wang et al. 2007). The ensemble mean was updated by the GSI-based hybrid system in which ensemble covariance information was incorporated. The initial ensemble perturbations were generated by the existing WRF DA system and updated by the ETKF in each DA cycle.
Section 2 briefly describes the hybrid DA system. Section 3 introduces the experimental design. Results of the track forecasts and fundamental analyses as well as some sensitivity tests are presented in section 4. Conclusions are given in section 5.
The hybrid GSI-ETKF system has two parts: (1) the GSI-based hybrid system for updating the ensemble mean, which was built on the existing GSI framework but could incorporate ensemble covariance information by modifying the original cost function and (2) the ETKF system (adopted from the WRFVAR) for updating ensemble perturbations. The updated ensemble perturbations were then added to the updated ensemble mean to obtain the analysis ensemble members required to initiate the ensemble forecast for the next cycle.
The standard GSI system adopted a 3DVAR cost function as
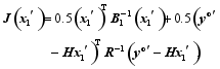
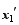
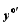
Incorporation of the ensemble information into the hybrid system and modification of the cost function were carried out using the following expression:
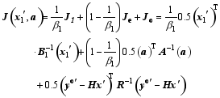
The analysis increment in the hybrid system, denoted as x′, then became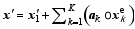
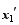
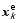
The background ensemble perturbations were updated using the ETKF method ( Wang and Bishop, 2003; Wang et al. , 2004, Wang et al.2007): Xa = XfT, (4)where the forecast perturbations Xfwere updated to the analysis perturbations Xa by a transform matrix T, which can be obtained from the following relation: T = C( ?+ I)-1/2, (5)where C and ? are, respectively, the eigenvector and eigenvalue matrices of ( Xf)T HT R-1 HXf/ K, and I is the identity matrix.
We applied the developed GSI-ETKF system to track forecast of typhoon Muifa cases in 2011. Muifa, the ninth typhoon in the northwest Pacific Ocean in 2011, was formed near 11.7°N, 135°E at 1400 UTC 28 July 2011. It became a super typhoon at 1800 UTC 2 August 2011 and kept moving westward in the following several days. Muifa recurved to the west-north and then to the north during the period from 0000 UTC 5 August 2011 to 0000 UTC 7 August 2011 and finally made landfall on the west coast of North Korea at 0000 UTC 8 August 2011 (Fig. 1).
In our study, the WRF 3.3 model with a single domain and 27-km resolution (254 × 226 grid points; 35 vertical levels) was used. The model physics included the WRF single-moment six-class (WSM) microphysics scheme, Kain-Fritsch cumulus parameterization scheme ( Kain and Fritsch, 1990), Yonsei University (YSU) boundary layer scheme ( Hong et al. , 2006), Rapid Radiative Transfer Model (RRTM) long wave scheme ( Mlawer et al. , 1997), and Dudhia shortwave scheme ( Dudhia, 1989).
To investigate the effects of hybrid GSI-ETKF system on TC initial field, especially on vortex location adjustment, it is necessary to have as many data as possible in the vortex and its steering flow areas. For this study, data were produced by simulating dropsonde observations in which temperature and wind profiles were generated by adding random noises to NCEP Global Forecast System (GFS) 0.5°×0.5° analysis field within the TC surrounding area (less than 10° away from the TC center, one profile for every eight WRF model grids). Random noises were generated using a Gaussian distribution with a mean of 0 and standard deviation of 1. A snapshot of the locations of simulated dropsonde at 1200 UTC 5 August 2011 is given in Fig. 2. Note that the observations were moving keeping pace with the movements of the TC.
Experiments were started at 0000 UTC 5 August, the beginning of the recurving stage of Muifa. Due to the model having of a limited-area domain, experiments were run for two assimilation cycles, each for six hours, to prevent the analysis from drifting away. After finishing two-cycle assimilations, the analyzed ensemble mean at 1200 UTC 5 August was used to initiate a single-member WRF forecast for 72 hours.
Three experiments were performed, each of them assimilating the same data without using any vortex bogussing or relocation approach. The standard GSI system was used for the first experiment (Exp1), and the correlation length scale and variance of the default static background error covariance matrix were tuned. The second experiment (Exp2) was carried out with the GSI-ETKF system in which three parameters were tuned: weighting factor 1/ β1for determining the weight to the static covariance, ensemble covariance localization scale Se, for deciding the localization scope of the ensemble covariance, and the number of ensemble member. We tested these three parameters and found that a combination of 1/ β1=0.0, Se= 707 km, and 32 ensemble members gave the best result. Exp2 included both the flow-dependent ensemble covariance in hybrid DA and the ensemble forecast, compared to Exp1. Hence, to separate the impacts of these two factors, we performed a third experiment (Exp3) by setting 1/ β1=1.0 in the hybrid system so that ensemble forecast could be included but not the ensemble covariance. The difference between Exp1 and Exp3 was that the former used a single deterministic forecast as the background forecast, whereas the latter used the ensemble mean for the same purpose. If the results of Exp1 and the Exp2 are found to be different while those of Exp1 and Exp3 are similar, it will suggest that this difference is mainly due to the flow-dependent covariance rather than the ensemble forecast.
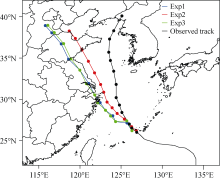 | Figure 1 The the CMA official best track (BABJ) best track and the track forecasts of three experiments of typhoon Muifa initialized with the analyses at 1200 UTC 5 August 2011. The every-six-hour position of TC during the forecast period is indicated by dots. The blue, red, and green lines represent the forecasts of Exp1, Exp2, and Exp3, respectively. |
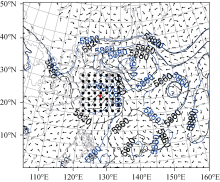 | Figure 2 Analyses of the 500-hPa geopotential height at 1200 UTC 5 August 2011 for Exp1 (black contour line) and Exp2 (blue contour lines). Arrows indicate the difference in the deep-layer (850-300 hPa) mean wind between Exp2 and Exp1. Positions of simulated dropsondes are indicated by black dots. The red typhoon symbol denotes the center of Muifa. |
Figure 1 shows the 72-hour track forecasts initialized at 1200 UTC 5 August 2011 after conducting two DA cycles for the three experiments, as well as the BABJ. During Exp1 and Exp3, the initial TC position and the consequent track forecast deflected westward compared to the best track; as a result, Muifa made land fall in Shanghai about 36 hours later. When the hybrid GSI-ETKF DA system was used with flow-dependent ensemble covariance, the initial vortex position and the track forecast were adjusted eastward and much closer to the observations in Exp2. In Exp2, track errors were reduced to 94, 245, and 595 km for forecasts at 24, 48, and 72 hours, respectively, as compared to those of 178, 368, and 816 km, respectively, in Exp1. In addition, results of Exp1 and Exp3 were similar, suggesting that the ensemble forecast hardly made any difference. Consequently, we focused on discussing the difference between Exp1 and Exp2 in the following sections.
In this section, detailed diagnostics are presented to explain why the track forecast with hybrid system is a better choice. Figure 3 shows the analysis increment of the 850-hPa geopotential height at 1200 UTC 5 August. For Exp1 (Fig. 3a), the analysis increment was isotropic and the TC position remained unchanged after the DA. In contrast, in Exp2, the analysis increment was flow dependent; negative increment was found to the east of the forecasted position which resulted in an eastward adjustment to the position. These results suggested that the flow-dependent ensemble covariance could correct the vortex position without using any other bogussing or relocation scheme, where as the static covariance in the standard GSI system could not. Chen and Snyder (2007) reported similar results in their study on assimilation of vortex position using an EnKF system.
Since the accuracy of TC track forecasts relies on the analyses of both the vortex and its surrounding environment, we further examined the analyzed environment fields. Figure 2 shows the analysis of the 500-hPa geopotential height at 1200 UTC 5 August 2011 for Exp1 and Exp2, as well as the difference in the deep-layer (850-300 hPa) mean wind between them. Muifa was embedded in the southwest periphery of the subtropical high. As compared to Exp1, the subtropical height of Exp2 was separated into two parts by another tropical storm named Merbok 2011 near 150°E and became square-toed. This difference in the two experiments suggested that, compared to Exp1, the subtropical high analyzed in Exp2 steered the TC more northward, resulting in a more east-ward track in the following-up forecast. To further confirm this hypothesis, we also calculated the difference in the deep-layer (850-300 hPa) mean wind between Exp2 and Exp1; a more eastward wind component to the southeast of Muifa could be identified consistently, which seemed to shift the track in Exp2 further to the east and produced a better track forecast.
Besides the environment, vertical structures of TCs were found to be different as well in the two experiments. Figure 4 shows the inner-core vertical structure of potential vorticity and wind speed distribution. It is clear from the figure that the potential vorticity extended higher above 12 km, and the maximum wind speed in the upper layer near 12 km was larger in Exp2 than in Exp1. This difference revealed that the hybrid GSI-ETKF system with the flow-dependent ensemble covariance obtained a deeper and intense TC compared to the standard GSI sys- tem.
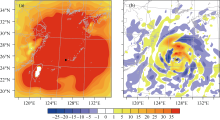 | Figure 3 Increments of 850-hPa geopotential height for (a) Exp1 and (b) Exp2 at 1200 UTC 5 August 2011. The square represents the background position of TC and the typhoon symbol represents the analysis position of TC. |
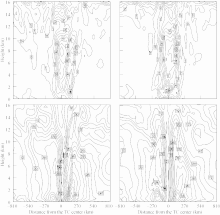 | Figure 4 West-east cross-section of potential vorticity (upper panel, units: PVU) and wind speed (bottom panel, units: m s-1) for the analyses in Exp1 (left column) and Exp2 (right column) at 1200 UTC 5 August 2011. |
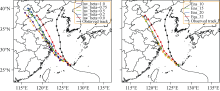 | Figure 5 Similar to Fig. 1, but showing the forecast tracks with different 1/ β1values by fixing the number of ensemble member to 32 (left) and with different numbers of ensemble members by fixing 1/ β1=0.0 (right). Here “Inv_beta” stands for the inverse of β1 coefficient (i. e. , 1/ β1). |
As mentioned above, several parameters were tuned to obtain the best result for the GSI-ETKF system. Here, we discuss in detail these sensitivity tests. Figure 5 (left) shows the track forecast sensitivity to the parameter 1/ β1, which determines the weight to the static covariance. It is clear from the figure that when more weight was given to the ensemble covariance, the model simulated the typhoon recurvature better. The parameter 1/ β1=0.0 gave the best result in terms of the Muifa track forecast. Figure 5 (right) illustrates the effect of the number of ensemble members on the track forecast. Three extra sensitivity experiments were performed by decreasing ensemble numbers from 32 (Ens_32) to 20 (Ens_20), 15 (Ens_15), and 10 (Ens_10), with 1/ β1=0.0. Obviously, Ens_32 gave the best results. However, although fewer ensemble members degraded the model forecast, the result of Ens_10 with 1/ β1=0.0 was better than that of Ens_32 with 1/ β1=1.0 with 32 members. These results suggested that the hybrid system was more sensitive to the weighting parameter 1/ β1 than the number of ensemble members. Further experiments with more cases and assimilation of real observations are needed to assess the generality of the results.
In this study, a hybrid GSI-ETKF DA system developed for the WRF model was applied to TC track forecasting for typhoon Muifa in 2011. By performing three different experiments, using the standard GSI system (Exp1), or using the hybrid system with the flow-dependent ensemble covariance (Exp2), or with the static covariance (Exp3) as the background covariance, the hybrid GSI-ETKF system was found to have a potential to improve the initialization and track prediction of TC. When the hybrid GSI-ETKF system was applied to typhoon Muifa cases, the track error of the 72-hour forecast was found to be less than 600 km, which was 200 km smaller than the track error associated with the standard GSI system. Further comparisons of the forecasts, analyses, and analysis increments between the hybrid system with the standard GSI system showed that such improvement was due to the flow-dependent ensemble covariance. These detailed diagnostics revealed that the hybrid GSI-ETKF system with the flow-dependent ensemble covariance was potentially able to adjust the position of the typhoon vortex, in addition to better updating the vortex vertical structure and the environmental field. Further sensitivity tests suggested that the hybrid system was more sensitive to the weighting parameter 1/ β1than to the number of ensemble members.
As a first attempt, these experiments were conducted at a coarse resolution (27 km) and only the simulated observations were assimilated. Our results were thus not a direct analog to the operational regional model forecasts, which had finer resolutions and denser observations. In future works, we will extend this research to more cases with higher resolution and real observation networks, so as to further explore the potential of the hybrid GSI-ETKF DA system in forecasting the TC track as well as its intensity.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|

