Cite this Article
JIA Bing-Hao, Ning ZENG, XIE Zheng-Hui. Assimilating the LAI Data to the VEGAS Model Using the Local Ensemble Transform Kalman Filter: An Observing System Simulation Experiment. Atmospheric and Oceanic Science Letters, 2014, 7(4): 314-319  
Permissions
Copyright?2014, Editorial office of Atmospheric and Oceanic Science Letters
This is an Open Access article under the terms of CCAL.
Assimilating the LAI Data to the VEGAS Model Using the Local Ensemble Transform Kalman Filter: An Observing System Simulation Experiment
JIA Bing-Hao1, Ning ZENG2, XIE Zheng-Hui1
1 State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
2 Department of Atmospheric and Oceanic Science & Earth System Science Interdisciplinary Center, University of Maryland, College Park, Maryland, USA
Abstract

Information on the spatial and temporal patterns of surface carbon flux is crucial to understanding of source/sink mechanisms and projection of future atmospheric CO2 concentrations and climate. This study presents the construction and implementation of a terrestrial carbon cycle data assimilation system based on a dynamic vegetation and terrestrial carbon model Vegetation-Glob- al-Atmosphere-Soil (VEGAS) with an advanced assimilation algorithm, the local ensemble transform Kalman filter (LETKF, hereafter LETKF-VEGAS). An observing system simulation experiment (OSSE) framework was designed to evaluate the reliability of this system, and numerical experiments conducted by the OSSE using leaf area index (LAI) observations suggest that the LETKF -VEGAS can improve the estimations of leaf carbon pool and LAI significantly, with reduced root mean square errors and increased correlation coefficients with true values, as compared to a control run without assimilation. Furthermore, the LETKF-VEGAS has the potential to provide more accurate estimations of the net primary productivity (NPP) and carbon flux to atmosphere (CFta).

Keyword: carbon cycle; data assimilation; VEGAS; land-atmosphere CO2 flux; LETKF; OSSE
1 Introduction

The understanding of carbon exchange between terrestrial ecosystems and the atmosphere can be improved through direct observations and experiments, as well as through modeling activities ( Yuan et al., 2009). Several terrestrial biosphere models, called forward models, have been developed to study the terrestrial carbon cycle and how the ecosystems respond to changes in climate and atmospheric CO2 concentration ( Chen et al., 1999; Zeng et al., 2005a; Thornton et al., 2007). However, forward modeling has large uncertainties due to various biased data sources and inaccurate parameterizations and parameters ( Piao et al., 2012).

Data assimilation has been applied to improve the terrestrial carbon cycle simulation by incorporating observational data into process-based models ( Wang et al., 2009; Luo et al., 2011). Rayner et al. (2005) developed a Carbon Cycle Data Assimilation System (CCDAS), which assimilated atmospheric CO2 concentration into a terrestrial biosphere model using the Bayesian approach. In addition, many studies have used this system to improve global carbon cycle simulation through assimilation of various data streams, mainly ground-based eddy covariance CO2 flux and remotely sensed data (e.g., the fraction of absorbed photosynthetically active radiation (fPAR)) on a global scale ( Scholze et al., 2007; Kato et al., 2013). However, the data assimilation frame used in the CCDAS needs to calculate the adjoint operator of the forecast model, and the computational cost would increase with adjoint.

Recently, a few studies have been conducted with encouraging results ( Mo et al., 2008; Gao et al., 2011) using an ensemble Kalman filter (EnKF) data assimilation algorithm, which does not require the adjoints of the model dynamics or observational operator, in the terrestrial carbon cycle data assimilation research. Unlike other EnKF schemes that assimilate observations serially, the local ensemble transform Kalman filter ( LETKF; Hunt et al., 2007) updates the local state variables of each grid point independently by assimilating all observations that may affect the state at that grid point. Moreover, the use of the localization approach in the LETKF makes this assimilation scheme highly parallel ( Szunyogh et al., 2007). Its computational efficiency, simplicity of implementation, and accuracy make the LETKF a particularly appealing EnKF scheme, and it has been used in the numerical weather forecast ( Miyoshi and Kunni, 2012) and atmospheric carbon cycle ( Kang et al., 2011). However, few studies have been conducted on the application of the LETKF algorithm in the terrestrial ecosystem research.

With this in mind, the LETKF algorithm is used to assimilate the leaf area index (LAI) observations into a dynamic vegetation and terrestrial carbon model, Vegetation-Global-Atmosphere-Soil (VEGAS; Zeng et al., 2004, 2005a, b), in this study. Our goal is to improve model-based terrestrial carbon cycle simulations (e.g., carbon pools and fluxes) through the assimilation of observational LAI data. Furthermore, we will investigate the effects of LAI observations on the terrestrial ecosystem components with different turnover times and the effect of vegetation types on assimilated results. In Section 2, a terrestrial carbon cycle data assimilation system based on the VEGAS model and the LETKF algorithm (hereafter LETKF-VEGAS) will be introduced. To evaluate the reliability and performance of the LETKF-VEGAS, an observational system simulation experiment (OSSE) frame- work will be designed and some preliminary results will be presented in Section 3.

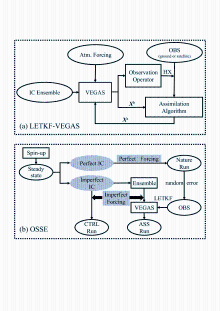
2 A terrestrial carbon cycle data assimilation system with LETKF-VEGAS

The terrestrial carbon cycle data assimilation system LETKF-VEGAS consists of a forecast operator VEGAS to simulate the terrestrial carbon cycle, an observational operator to map the model state vector into observation vector space by providing model equivalents of the observed values ( Bouttier and Courtier, 1999), and an ensemble-based LETKF assimilation algorithm to optimize the state variables. A sketch of the LETKF-VEGAS is shown in Fig. 1a.

2.1 Model: VEGAS

The VEGAS model ( Zeng et al., 2004, 2005a, b) can simulate the dynamics of vegetation growth and competition among different plant functional types (PFTs). It includes four PFTs (namely, broadleaf tree, needleleaf tree, cold grass, and warm grass), among which the competition is determined by climatic constraints and resource allocation strategy such as temperature tolerance and height-dependent shading. The vegetation module in VEGAS is coupled to a two-layer physical land surface model Simple-Land (SLand) ( Zeng et al., 2005a).

The VEGAS model includes five vegetation pools: leaf ( Cleaf), fine root ( Crootf), coarse root ( Crootc), sapwood ( Cwoods), and heartwood ( Cwoodh) and six soil carbon pools: metabolic litter ( Clmeta), structural litter ( Clstru), fast soil ( Csfast), intermediate soil ( Csmed), slow soil ( Csslow), and decomposer ( Cdcmp). The carbon balance of each carbon pool can be described using the following generic biomass equation, involvingpools and fluxes (sometimes termed as stocks and flows):

(1)

(2)

where C is the carbon pool size per unit area and Fin and Fout are the carbon flux into and out of the pool, respectively. The loss terms include the following: r represents respiration, t is turnover to other pools, b is background mortality due to natural loss or disturbance, s represents loss due to cold, drought and other stresses, f is loss due to fire. We use Eq. (1) to forecast dynamically the terrestrial carbon cycle.

The key carbon flux outputs from the VEGAS model are related as follows:

(3)

(4)

(5)

where the gross primary productivity (GPP) is the total amount of carbon fixed the terrestrial ecosystem through photosynthesis; NPP is the net primary productivity; Ra and Rh are autotrophic respiration and heterotrophic respiration, respectively; and NEP is the net ecosystem production. We do not consider the contribution of anthropogenic effects to the VEGAS model; hence, the carbon flux to atmosphere (CFta) is referred to as the net ecosystem exchange (NEE).

The physical climate forcing input to VEGAS includes surface temperature, precipitation, atmospheric humidity, radiation forcing, and surface wind. For this study, the driving data of precipitation for VEGAS have been collected from a combination of the Climate Research Unit ( Mitchell and Jones, 2005) and the Xie and Arkin (1996) data set. Data on the surface air temperature and surface downward solar radiation have been taken from the National Aeronautics and Space Administration (NASA) Goddard Institute for Space Studies ( Hansen et al., 1999) and the Multi-scale Synthesis and Terrestrial Model Intercomparison Project (http://nacp.ornl.gov/MsTMIP.shtm), respectively. Seasonal climatology of humidity and wind speed were used in this study ( Qian et al., 2008).

2.2 LETKF algorithm

The LETKF algorithm ( Hunt et al., 2007) is an advanced square-root EnKF data assimilation scheme, in which observations are assimilated simultaneously to update the ensemble mean, while the ensemble perturbations are updated by transforming the forecast perturbations through a transform matrix term. It assimilates all observations within a certain distance at all analysis grid points simultaneously ( Hunt et al., 2007). In the LETKF algorithm, the analysis ensemble mean and ensemble perturbations can be expressed as follows:

(6)

(7)

(8)

(9)

(10)

where is the mean of the background ensemble members; is a matrix whose columns are the background perturbations , where N is the ensemble size); w is a Gaussian random vector with mean 0 and covariance , while and are transformed vectors corresponding to ensemble mean and perturbations; is the analysis error covariance in the forecast perturbation space; is a multiplicative inflation parameter; is a vector of all the observations; and is a vector of background ensemble mean and perturbations in the observation space, respectively, where H is an observation operator that transforms the state variable from the model space to the observation space; and R is the observation error covariance. The global analysis ensemble ( i=1,..., N) is formed by gathering the values obtained for (Eq. (6)) and (Eq. (8)) at all the analysis grid points. For more details and discussion on LETKF, see Hunt et al. (2007). In the LETKF-VEGAS, 11 prognostic variables (carbon pools) are used to form the state vector in LETKF, which includes five vegetation carbon pools and six soil carbon pools.

2.3 Main descriptions of LETKF-VEGAS

In this study, we demonstrate a framework for the assimilation of LAI observations using the LETKF-VEGAS to update VEGAS-simulated carbon pools. As in the VEGAS model, there is a linear relationship between LAI and leaf carbon, which is expressed as follows:

(11)

where is the specific leaf area in m2 kg-1 C-1 with the following values: broadleaf tree 30, needleleaf tree 10, cold grass 20, and warm grass 35 ( Dickinson et al., 1998). Here, Eq. (11) is considered as the observational operator H in LETKF. In practice, LAI would affect the gross photosynthetic rate and carbon allocation in VEGAS ( Zeng et al., 2005a). The accuracy of the analyzed prognostic variables depends on the accuracy of the estimated background error covariances and on the information provided by observations.

3 The OSSE
3.1 Experimental design

To evaluate the reliability of the LETKF-VEGAS, we conducted an OSSE using a set of synthetic data ( Gao et al., 2011; Kang et al., 2011). The OSSE framework was developed through twin experiments, in which the forecast model simulation, forced by the perfect initial condition (IC) and atmospheric forcing, was defined as the "nature" run and served as the true state of the OSSE to compare with the pure simulation or assimilation model run with imperfect IC and atmospheric forcing. Here, we assume that the prediction model and observation operator are perfect, an assumption that has been used in many earlier OSSE studies ( Tong and Xue, 2005; Xue et al., 2006; Kang et al., 2011). Model error will be an issue for future studies.

Figure 1b shows the flowchart of the OSSE. VEGAS was first spin-up run using the 1901 climate forcing repeatedly until the carbon pools reached equilibrium (steady state) ( Zeng et al., 2005a; Qian et al., 2008). This state was then used as the IC for the 1901-1992 run. For performing comparisons and analyses in this study, we focused only on the period of 1991-1992 in view of the reliability of LETKF-VEGAS. Here, the two-year (1991-1992) simulation was chosen as the nature run. The observational LAI data were generated from the nature run by selecting a 10-day (close to the temporal resolution of satellite-retrieved LAI, e.g., eight days for the Moderate Resolution Imaging Spectroradiometer (MODIS)) sampled time series of the data and adding random noise at a scale of 0.05 to represent observational errors. All the observations are assumed to be available during the experimental period.

Figure 1 (a) Sketch of the LETKF-VEGAS, and (b) diagram of the observing system simulation experiment (OSSE) used in this study. Ovals represent input and output data, and boxes represent calculation steps. IC represents initial condition; CTRL and ASS are control and assimilation experiments, respectively.

Unlike the nature run, we chose an imperfect IC and atmospheric forcing to run VEGAS for the period of 1991-1992 in the control or assimilation experiments. The imperfect atmospheric forcing was generated using a climatological mean (without any interannual variation). The imperfect IC for the control run was chosen randomly from historical simulations. As the LETKF is one of the ensemble-based assimilation algorithms, the initial ensemble members (background) were also chosen by random sampling from historical long-term simulations ( Kang et al., 2011). It should be noted that VEGAS was operated on a daily time step at 2.5°×2.5° resolution for all experiments in this study. The focus of this study is the natural land-atmosphere fluxes. Therefore, land-use change is not included in the VEGAS model ( Zeng et al., 2004, 2005a).

The ensemble size ( N) is an important parameter in EnKF and should be large enough to ensure a correct estimate of the error covariance in the predicted model states ( Williams et al., 2005). However, a very large ensemble size may introduce a heavy computation burden. In this study, the ensemble size was set to 80 ( Mo et al., 2008).

3.2 Performance of LETKF-VEGAS

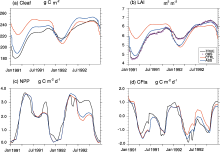
We randomly chose a site (33.75°N, 91.25°W) in North America to evaluate the performance of the LETKF- VEGAS. The dominant PFT at this site is broadleaf tree and its climate type is temperate (Table 1). Figure 2 shows the time series of leaf carbon pool ( Cleaf), LAI, NPP, and CFta based on the data from nature run (TRUE), control run (CTRL), and assimilation model run (ASS). The observational LAI data (OBS) are also presented in Fig. 2b. It is readily found that the LETKF-VEGAS is capable of improving model-based leaf carbon pool due to the assimilation of LAI observations and of providing more accurate LAI estimations. Table 2 shows that the assimilated Cleaf is closer to true values with smaller root mean square error (RMSE = 8.4 g C m-2) and higher correlation ( r = 0.97), compared to the CTRL (RMSE = 20.3 g C m-2 and r = 0.50). LAI estimations from the LETKF-VEGAS also improved significantly due to their close relationship with Cleaf with reduced RMSE (0.19 g C m-2), as compared to CTRL (RMSE = 0.53 g C m-2) (Fig. 2b and Table 2). Moreover, the control run could not capture well the temporal variation of true LAI values ( r = 0.49) during the experimental period, which shows similar seasonal variations for the two years ( from 1991 to 1992) due to the effect of imperfect atmospheric forcing without any interannual variation. However, obvious improvement is observed in ASS with a higher correlation ( r = 0.95) with TRUE.

Table 1 Site characteristics of this study.

Figure 2 Time series of daily mean (a) leaf carbon pool ( Cleaf), (b) leaf area index (LAI), (c) net primary productivity (NPP), and (d) carbon flux to atmosphere (CFta) from nature run (TRUE), observational data (OBS), CTRL, and ASS conducted from January 1991 to December 1992 at the site (33.75°N, 91.25°W).

However, the improvement in assimilated soil carbon pools is not as much as that in the leaf carbon pool (not shown in this study), which may be due to that observed LAI data contribute less information on the carbon pools with a slow turnover time ( Zeng et al., 2005b; Weng et al., 2011). As long-running forest stem surveys and tree ring data could provide an important constraint on C cycling of slow pools, how to implement the assimilation of these data in the LETKF-VEGAS will be a topic of our future studies.

Since carbon fluxes usually act as diagnostic variables in the VEGAS model, they are not changed by the analysis step of data assimilation in the LETKF-VEGAS and updated only by the model forecast using analyzed state variables from data assimilation. Here, we will discuss the effect of the assimilation of LAI observations on carbon fluxes using the LETKF-VEGAS. Due to an improvement in state variables (e.g., Cleaf), simulations of NPP and CFta made by the LETKF-VEGAS match true values better than the control run (Figs. 2c and 2d), with lower RMSEs of 0.49 g C m-2 d-1 (NPP) and 0.35 g C m-2 d-1 (CFta), respectively. It can be also found from Table 2 that assimilated NPP and CFta have higher correlation coeffi-cients ( r = 0.94 and 0.91, respectively) with true values, compared to those from control run ( r = 0.92 and 0.88, respectively).

Table 2 The root mean square errors (RMSEs) and correlation coefficients ( r) between model simulations and true values from nature run for the four variables ( Cleaf, LAI, NPP, and CFta) during the experimental period (1991-1992) at the broadleaf tree site (33.75°N, 91.25°W).
3.3 Evaluation under different PFTs

To gain further insights into the effect of PFTs on the assimilated results, three other sites, which represent needleleaf tree (NLT), cold grass (CG), and warm grass (WG), were chosen to evaluate the performance of the LETKF-VEGAS under different vegetation types. Characteristics of these sites are presented in Table 1. Figure 3 shows the mean bias errors (MBEs), RMSEs, and correlation coefficients between the simulated (CTRL and ASS) daily Cleaf (Figs. 3a-c) and LAI (Figs. 3d-f) and true values from nature run over four PFTs from 1991 to 1992. It can easily be observed that the LETKF-VEGAS can improve the model simulations of Cleaf and LAI significantly for different PFTs. For the WG site, the assimilated Cleafshows a lower bias (1.6 g C m-2) and RMSE (1.9 g C m-2) (Figs. 3a and 3b) to true values, compared to the control run (MBE = 5.9 g C m-2 and RMSE = 12.8 g C m-2). Moreover, the LETKF-VEGAS has a higher correlation ( r = 0.93) with true values, while that with CTRL is only 0.58 (Fig. 3c). Similar results could be observed for LAI values at this site (Figs. 3d-f). It can also be seen from Figure 3 The mean bias errors (MBEs, RMSEs, and correlation coefficients between the simulated daily Cleaf (a-c) and LAI (d-f) and true values from nature run over four PFTs (defined in Table 1) from January 1991 to December 1992. CTRL is the control run without assimilation, and ASS is the assimilated results from the LETKF-VEGAS.

Fig. 3 that the LETKF-VEGAS has similar correlation coefficients with true values to the control run for both Cleaf and LAI at the NLT and CG sites. This may be due to that CTRL exhibits higher correlations with TRUE, which leads to a little improvement space for the LETKF- VEGAS. However, compared to CTRL, the LETKF- VEGAS reduces the biases significantly (Fig. 3).

4 Summary and discussions

In this study, a terrestrial carbon cycle data assimilation system with the LETKF-VEGAS was developed, and an OSSE framework was designed to evaluate the reliability of the system. Preliminary results are promising as they show that the LETKF-VEGAS works effectively and is capable of improving significantly the model-based leaf carbon pool through the assimilation of observational LAI data over all four PFTs. However, observed LAI data have weak constraints on the estimates of other components of the carbon cycle with slow turnover times (e.g ., soil carbon pool), which leads to only slight improvement in these carbon pools. Due to the improvement of state variables (e.g., Cleaf), simulations of LAI and some key carbon fluxes (e.g., NPP and CFta) performed using the LETKF-VEGAS match true values better than control run simulations without assimilation.

As the design of the LETKF-VEGAS is flexible to include further streams of observational data (e.g., eddy flux measurements and satellite-derived fPAR), these data will be assimilated to VEGAS model through different observational operators using the LETKF-VEGAS ( Gao et al., 2011; Kato et al., 2013). In addition, parameters in the processed ecosystem model have large uncertainties due to the complexity of ecosystem processes, especially for those that could not be measured directly in the field ( Mo et al., 2008). Our future study will focus on the implementation of simultaneous optimizations of state variables and model parameters using the LETKF algorithm in the LETKF-VEGAS.

Acknowledgements. This research was supported by the National Natural Science Foundation of China (Grant No. 41305066), the Special Funds for Public Welfare of China (Grant No. GYHY201306045), and the National Basic Research Program of China (Grant Nos. 2010CB951101 and 2010CB428403). We would particularly like to thank Fang ZHAO, Dr. Eugenia KALNAY, Dr. Takemasa MIYOSHI, Dr. Ji-Sun KANG and Dr. Steven GREYBUSH for their helpful comments. We also thank two anonymous reviewers for constructive comments and suggestions, which have helped us in improving the paper.

Reference
1 Bouttier F. , P. Courtier, 1999: Data Assimilation Concepts and Methods, European Centre for Medium-Range Weather Forecasts Meteorological Training Course Lecture Series, Reading, 59pp.
2 Chen J. M. , J. Liu, J. Cihlar, et al. , 1999: Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications, Ecol. Model. , 124, 99-119.
3 Dickinson R. E. , M. Shaikh, R. Bryant, et al. , 1998: Interactive canopies for a climate model, J. Climate, 11, 2823-2836.
4 Gao C. , H. Wang, E. S. Weng, et al. , 2011: Assimilation of multiple data sets with the ensemble Kalman filter to improve forecasts of forest carbon dynamics, Ecol. Appl. , 21(5), 1461-1473.
5 Hansen J. , R. Ruedy, J. Glascoe, et al. , 1999: GISS analysis of surface temperature change, J. Geophys. Res. , 104, 30997-31022.
6 Hunt B. R. , E. Kostelich, I. Szunyogh, 2007: Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter, Physica D, 230, 112-126, doi: DOI:10.1016/j.physd.2006.11.008.
7 Kang J. S. , E. Kalnay, J. Liu, et al. , 2011: ˇ°Variable localizationˇ± in an ensemble Kalman filter: Application to the carbon cycle data assimilation, J. Geophys. Res. , 116, D09110, doi: DOI:10.1029/2010JD014673.
8 Kato T. , W. Knorr, M. Scholze, et al. , 2013: Simultaneous assimilation of satellite and eddy covariance data for improving terrestrial water and carbon simulations at a semi-arid woodland site in Botswana, Biogeosciences, 10, 789-802.
9 Luo Y. Q. , K. Ogle, C. Tucker, et al. , 2011: Ecological forecasting and data assimilation in a data-rich era, Ecol. Appl. , 21(5), 1429-1442.
10 Mitchell T. D. , P. D. Jones, 2005: An improved method of constructing a database of monthly climate observations and associated high-resolution grids, Int. J. Climatol. , 25, 693-712.
11 Miyoshi T. , M. Kunii, 2012: The local ensemble transform Kalman filter with the Weather Research and Forecasting model: experiments with real observations, Pure Appl. Geophys. , 169, 321-333.
12 Mo X. , J. M. Chen, W. Ju, et al. , 2008: Optimization of ecosystem model parameters through assimilating eddy covariance flux data with an ensemble Kalman filter, Ecol. Model. , 217(1), 157-173.
13 Piao S. L. , A. Ito, S. G. Li, et al. , 2012: The carbon budget of terrestrial ecosystems in East Asia over the last two decades, Biogeosciences, 9, 3571-3586.
14 Qian H. , R. Joseph, N. Zeng, 2008: Response of the terrestrial carbon cycle to the El Niño-Southern Oscillation, Tellus, 60B, 537-550.
15 Rayner P. , M. Scholze, W. Knorr, et al. , 2005: Two decades of terrestrial Carbon fluxes from a Carbon Cycle Data Assimilation System (CCDAS), Global Biogeochem. Cycles, 19, GB2026, doi: DOI:10.1029/2004GB002254.
16 Scholze M. , T. Kaminski, P. Rayner, et al. , 2007: Propagating uncertainty through prognostic carbon cycle data assimilation system simulations, J. Geophys. Res. , 112, D17305, doi: DOI:10.1029/2007JD008642.
17 Szunyogh I. , E. J. Kostelich, G. Gyarmati, et al. , 2007: A local ensemble transform Kalman filter data assimilation system for the NCEP global model, Tellus A, 60, 113-130.
18 Thornton P. E. , J. F. Lamarque, N. A. Rosenbloom, et al. , 2007: Influence of carbon-nitrogen cycle coupling on land model response to CO2 fertilization and climate variability, Glob. Biogeochem. Cycles, 21, GB4018, doi: DOI:10.1029/2006GB002868.
19 Tong M. , M. Xue, 2005: Ensemble Kalman filter assimilation of Doppler radar data with a compressible nonhydrostatic model: OSS experiments, Mon. Wea. Rev. , 133, 1789-1807.
20 Wang Y. P. , C. M. Trudinger, I. G. Enting, 2009: A review of applications of model-data fusion to studies of terrestrial carbon fluxes at different scales, Agric. Forest Meteor. , 149, 1829-1842.
21 Weng E. S. , Y. Q. Luo, C. Gao, et al. , 2011: Uncertainty analysis of forest carbon sink forecast with varying measurement errors: A data assimilation approach, J. Plant Ecol. , 4(3), 178-191.
22 Williams M. , P. A. Schwarz, B. E. Law, et al. , 2005: An improved analysis of forest carbon dynamics using data assimilation, Glob. Change Biol. , 11, 89-105.
23 Xie P. , P. A. Arkin, 1996: Analyses of global monthly precipitation using gauge observations, satellite estimates, and numerical model predictions, J. Climate, 9, 840-858.
24 Xue M. , M. Tong, K. K. Droegemeier, et al. , 2006: An OSSE framework based on the ensemble square-root Kalman filter for evaluating the impact of data from Radar networks on thunderstorm analysis and forecasting, J. Atmos. Oceanic Technol. , 23, 46-66.
25 Yuan W. P. , Y. Q. Luo, A. D. Richardson, et al. , 2009: Latitudinal patterns of magnitude and interannual variability in net ecosystem exchange regulated by biological and environmental variables, Glob. Change Biol. , 15, 2905-2920, doi: DOI:10.1111/j.1365-2486.2009.01870.x.
26 Zeng N. , A. Mariotti, P. Wetzel, 2005a: Terrestrial mechanisms of interannual CO2 variability, Glob. Biogeochem. Cycles, 19, GB1016, doi: DOI:10.1029/2004GB002273.
27 Zeng N. , H. Qian, E. Munoz, et al. , 2004: How strong is carbon cycle-climate feedback under global warming?Geophys. Res. Lett. , 31, L20203, doi: DOI:10.1029/2004GL020904.
28 Zeng N. , H. F. Qian, C. Roedenbeck, et al. , 2005b: Impact of 1998-2002 midlatitude drought and warming on terrestrial ecosystem and the global carbon cycle, Geophys. Res. Lett. , 32, L22709, doi: DOI:10.1029/2005GL024607.