The effects of precipitation on the moist potential vorticity substance (MPVS) are investigated by analyzing the MPVS with precipitation mass forcing and its impermeability in daily 1° × 1° data of the National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR) over the Yangtze River Basin from 21 June to 2 July 1999. The results show that the positive MPVS anomalies appear mainly along the Mei-yu front, where the maximum MPVS collocates with the maximum surface rainfall. Rain case diagnoses indicate that the MPVS anomaly may be used as a dynamical signal to detect the location and shift of the rain band when its impermeability is considered.
Potential vorticity (defined as 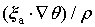
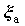
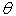
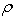
In torrential rain systems, however, the atmosphere is nearly saturated, and therefore moist potential vorticity (defined as 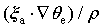
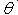
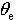
Importantly, the conservation and invertibility of PV may not be held in torrential rain systems, whose flow is not frictionless, adiabatic, and balanced, whereas the impermeability of PV substance (PVS) is kept. The impermeability of the PVS means that PVS cannot cross isentropic surfaces (Haynes and McIntyre, 1987, 1990). Schubert et al. (2001) introduced a PV principle for a non-hydrostatic, moist, precipitating atmosphere, and simply discussed the impermeability principle of PVS. The question is: can the impermeability of PVS be used to diagnose weather phenomena?
It is well known that a large amount of water vapor will be condensed into raindrops that fall down to the ground as precipitation when torrential rain occurs. This mass reduction of water vapor in moist atmosphere is called mass forcing (or mass sink). Qiu et al. (1993) showed that the precipitation-induced mass forcing is not negligible in commonly used numerical models, but they did not examine the impacts of the mass forcing on dynamic and thermodynamic processes. It would also be interesting to know whether the mass forcing can cause any anomaly of the moist PVS (MPVS in torrential rain systems) and whether the anomaly of MPVS can be used to diagnose the location and orientation of the rain band when its impermeability is considered.
In this study, the impermeability of MPVS with mass forcing is proven from primitive atmospheric dynamic equations (see Appendix). The MPVS equation with mass forcing is derived in section 2, and its diagnosis with torrential rainfall along the Mei-yu front during the mature Mei-yu period in 1999 in China is presented in section 3. A summary and discussion is provided in section 4.
The continuity equations can be written by
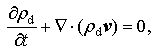 |
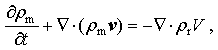 |
where 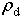
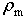
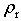
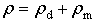
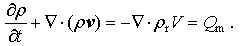
Here, v is the velocity of moist air, V is the terminal velocity of raindrops, and Q means the mass forcing termand the right term in Eq. (2) and Eq. (3) include the mass forcing term caused by the fall of raindrops.
The vorticity and thermodynamics equations can be expressed by
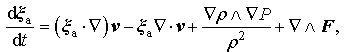 |
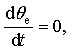 |
where 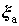
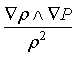
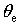
Taking 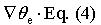
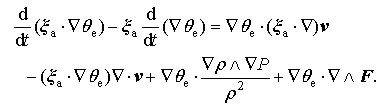 |
The use of the coincidence relation that
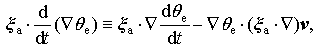 |
and Eq. (5) in Eq. (6) yields
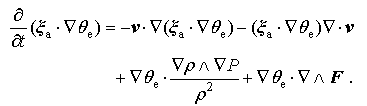 |
By using the continuity equation
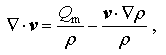
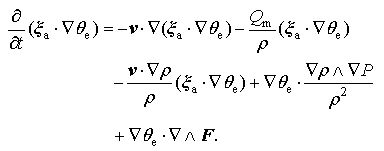 |
Here, 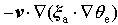
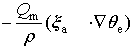
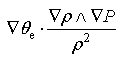
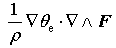
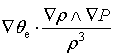
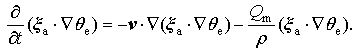 |
Thus, the advection and mass forcing are the two major contributors to the tendency of MPVS in torrential rain systems; and in this paper, we focus only on analyzing the contribution of the mass forcing and in the following discussion.
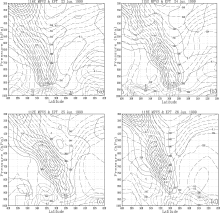
Having theoretically derived the MPVS equation with mass forcing, we now turn to ensuring whether or not there are MPVS anomalies when torrential rain occurs. For this purpose, by using daily 1° × 1° data of the National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR), the distribution of MPVS during the mature Mei-yu period from 21 June to 2 July 1999 is diagnosed. Figure 1 presents the vertical-meridional cross section of MPVS. During this Mei-yu period, the large positive centers of MPVS anomalies mainly collocate with the large values of potential temperature gradients near the Mei-yu front. The MPVS anomalies mainly occur between 900 hPa and 500 hPa. This indicates that the MPVS anomalies with mass forcing appear during the rainfall period. In Fig. 1, the MPVS is negative below 900 hPa along the front, which might be due to boundary process effects. However, this is not the focus of the present paper; we concentrate on the positive region above that level. It can also be seen that positive MPVS anomaly centers with the value of 0.8 collocate with the Mei-yu front; in particular, the anomaly centers generally appear at 700 hPa. Thus, the MPVS anomaly at 700 hPa is analyzed next.
Similar to the impermeability of PVS, the MPVS also has impermeability. Thus, the MPVS anomaly induced by precipitation can be used in torrential rainfall considering its impermeability. The iso-θ e lines can be drawn directly on certain constant pressure surfaces; thus, the iso-θ e lines on one constant pressure surface signify the cross lines between the moist isentropic surface and the isobaric surface. The MPVS anomaly between the two chosen moist isentropic surfaces must move in this moist isentropic tube, i.e., they must move along these two iso-θ e lines on some isobaric surfaces. Because the MPVS anomaly induced by precipitation represents the rain region, its location and shift can show the propagation of the rain band. Therefore, it provides a scientific foundation to use the orientation of movement of the MPVS anomaly for predicting the location and shift of the torrential rain band. In summary, the orientation and location of the rain band can be predicted by focusing on the distribution of iso-θ e lines and the allocation of the MPVS anomaly on synoptic maps.
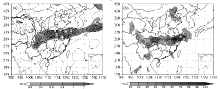
At 0000 UTC 23 June 1999, a southwest-northeast oriented MPVS anomaly occurs over the Yangtze River Basin, whose centers are located between 105° E and 110° E at 30° N, with a maximum MPVS value of 0.8 (Fig. 2a). Correspondingly, a rain band with the same orientation appears, and the biggest precipitation center is a little north of the MPVS center because of both the baroclinicity of the synoptic system and the influence of advection induced by southwesterly flow on the rainfall (Fig. 2b). This indicates that the MPVS anomaly region is associated with the rain band. Figure 2a also shows that the iso-θ e lines on both sides of the MPVS anomaly region are also southwest-northeast oriented, which indicates that the MPVS anomaly region will maintain the southwest-northeast orientation according to its impermeability, and the related rain band causing the MPVS anomaly should also possess the same orientation.
The collocation between the high MPVS anomaly region over the Yangtze River Basin and the rain band can be seen more clearly in Fig. 3. It shows that a southwest-northeast oriented MPVS anomaly remains near to and east of the Yangtze River Basin, while its centers are in the previous locations with a value of MPVS larger than 1.0. Furthermore, the precipitation centers in Fig. 3b also show that an observed precipitation center of 100 mm actually exists along the Yangtze River near 118° E, which is in a similar location to the MPVS anomaly. It also shows that there is a region of rainfall centers of 50-60 mm between 110° E and 115° E, and that they too are southwest-northeast oriented. The iso-θ e lines along both sides of the MPVS anomaly region still take on a southwest-west orientation, and the MPVS anomaly region orients southwest-northeast, which is parallel to the iso-θ e lines (Fig. 3a), indicating that the orientation of the future MPVS anomaly will still maintain a southwest-west orientation, the same as the iso-θ e line distribution. Furthermore, the rain band will also maintain a southwest-west orientation.
At 0000 UTC 25 June, an MPVS anomaly region remains from east of the Tibetan Plateau through the Yangtze River to the southwest of Japan (Fig. 4a), and its centers between 110° E and 130° E at 30° N have shifted from a southwest-northeast orientation on 24 June to a southwest-west orientation. Meanwhile, Fig. 4b reveals that the rain band is still in a southwest-northeast orientation. However, the iso-θ e lines along the MPVS anomaly region have already diverted from a southwest-northeast to a nearly east-west orientation, which indicates that the MPVS anomaly region will also adjust to an east-west orientation in the future, as will the rain band based on the MPVS impermeability. On 26 June, both the rain band and the MPVS anomaly region do indeed change from a southwest-northeast to an east-west orientation (Fig. 5), which is the same as the prediction according to the MPVS anomaly region and the direction of iso-θ e lines on 25 June.
From 26-30 June, the rain band over the Yangtze River in China maintains an east-west orientation with its centers located along the Yangtze River Basin (figures not shown). Correspondingly, the MPVS anomaly remains at the same orientation, and the distributions of its centers are similar to those of precipitation at around 110-130° E at 30° N. The MPVS anomaly is parallel to the iso-θ e lines, which further proves the impermeability theorem of MPVS.
Due to the impermeability of MPVS, the MPVS anomaly region associated with rainfall must be limited between the two certain iso-θ e lines. What interests us more is not only that the MPVS between the iso-θ e lines can shift its distribution to allow for the change of the iso-θ e lines, but the distribution of the torrential rain band also changes its location and orientation with the MPVS anomaly region and the iso-θ e lines. This provides an important clue to forecasting the position and shift of torrential rain bands using the high MPVS centers and direction of the iso-θ e lines.
In summary, the MPVS anomaly induced by precipitation mass forcing can be used as a signal to predict the region of the torrential rain band, and then the angle between the MPVS anomaly region and the potential temperature 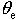
The effects of precipitation on the moist potential vorticity substance are investigated by analyzing the MPVS with precipitation mass forcing. It is found that torrential rain can cause an obvious MPVS anomaly which, combined with its impermeability, may be used to detect the location and shift of the rain band. A torrential rainfall case over the Yangtze River Basin from 21 June to 2 July 1999 is illustrated. The case study shows that the rain band coincides with the MPVS anomaly region, and therefore this anomaly is a good dynamical signal for indicating the location and shift of the torrential rain band. It is a useful supplement to the traditional method of using the troughs and ridges on synoptic maps to predict the torrential rain band. However, it is important to note that in Figs. 2-5, to some extent, the location of the main MPVS band lies north of the main 24-h rain band. This difference is likely due to the fact that the MPVS is at the 700 hPa level but the rainfall is at the surface.
The MPVS (Q in the following discussions) equation can be written as: 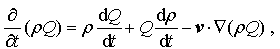
substituting Eqs. (3) and (6) into Eq. (A.1) leads to
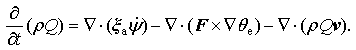
Let 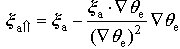
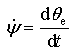
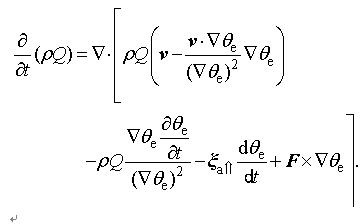
Let 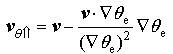
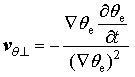
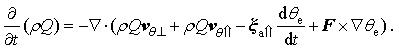
The first term 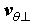
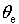
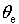
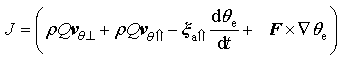 yields
yields
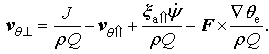
It can be seen from this equation that if MPVS moves at a speed of 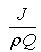
Equation (A.4) can be written as
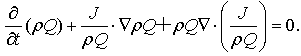
Because MPVS should satisfy substance conservation equation, it can be written
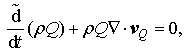
where the substantial derivative for MPVS is 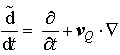
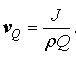
Thus, the velocity of MPVS should be 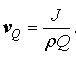
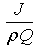
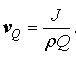
Acknowledgments
This work was supported by the National Basic Research Program of China (Grant No. 2014CB441402) and the National Natural Science Foundation of China (Grant Nos. 41275065, 41475054, and 41075044).
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|