FGOALS-s2 is one of the member models of the Coupled Model Intercomparison Project Phase 5 (CMIP5). Its atmospheric component is version 2 of the Spectral Atmospheric Model of the State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG), Institute of Atmospheric Physics (IAP) (SAMIL2) (Wu et al., 1996), with a horizontal resolution of R42 (approximately 1.66° (latitude) × 2.81° (longitude)), and 26 vertical levels. The oceanic component is version 2 of the LASG/IAP Climate Ocean Model (LICOM2), with a 1° resolution in the horizontal direction (0.5° meridional resolution in the tropics), and 30 vertical levels (Liu et al., 2012). The land and sea ice components are version 3 of the Community Land Model (CLM3) (Oleson et al., 2004) and version 5 of the Community Sea Ice Model (CSIM5) (Briegleb et al., 2004), respectively. The four components are coupled through a flux coupler (Collins et al., 2006). More detailed descriptions of the model can be found in Bao et al. (2013).

The European Center for Medium-Range Weather Forecasts (ECMWF) Re-Analysis Interim (ERA-Interim) dataset (Dee et al., 2011) covers the period from 1979 to the present day, with a horizontal resolution of 1.5° (longitude) × 1.5° (latitude) and 37 pressure levels from 1000 to 1 hPa. The CMIP5 historical run of FGOALS-s2 covers the period from 1850 to 2005. The model biases are defined as the differences in the climatological mean fields between FGOALS-s2 and ERA-Interim during 1979- 2005.

Based on the energy balance within a multi-layer surface-atmosphere column, the difference ( ) in energy balance between the two equilibrium states (model and ERA-Interim) in CFRAM can be written as

, (1)

where and are the differences in divergence of the longwave radiation flux and the convergence of shortwave radiation flux from the ERA-Interim to the FGOALS-s2 climatological mean state, respectively. represents the difference in the convergence of total energy flux due to non-radiative processes. It includes the energy flux difference due to surface sensible heat flux ( ), surface latent heat flux ( ), dynamic processes ( ) including net energy convergence at the surface (i.e., land and oceanic surface energy transport and energy storage, mainly in the oceans), and dynamic processes in the atmosphere at all scales ( ) including turbulence, convection, and large-scale atmospheric motions:

. (2)

and can be linearly decomposed into the sum of partial energy perturbations due to changes in individual radiative processes, such as incoming solar radiation at the top of the atmosphere (TOA) (o), ozone (O₃), water vapor (w), cloud (c), and surface albedo ( ):

, (3)

, (4)

where is the Planck feedback matrix whose jth column corresponds to the vertical profile of the radiative energy perturbation due to a 1 K warming in the jth layer from ERA-Interim to FGOALS-s2; and represents the difference in divergence of the longwave radiation energy flux due to the temperature difference itself ( ). The Fu-Liou radiative transfer model (Fu and Liou, 1992, 1993) is applied in CFRAM to calculate the radiative energy perturbation terms and the Planck feedback matrix.

Substituting Eqs. (2)-(4) into Eq. (1), and rearranging the terms and multiplying both sides of the resultant equation by , we obtain

. (5)

Equation (5) states that the local temperature difference (including T_s and T_a) at each grid point between FGOALS-s2 and ERA-Interim ( ) can be directly attributed to the model biases in representing the radiative processes including (left to right in Eq. (5)) incident solar radiation at the TOA, ozone, water vapor, cloud, surface albedo, and non-radiative processes including surface sensible heat flux, surface latent heat flux, surface dynamics, and atmospheric dynamics. Note that what we use in this study is the linear version of the CFRAM because of its much lower computational cost than the nonlinear version, and the very close results between them (Cai and Lu, 2009). All the CFRAM calculations are performed grid-by-grid before the global or zonal averages are taken. More details of the CFRAM formulation for this attribution analysis can be found in Yang et al. (2015) and Ren et al. (2015).

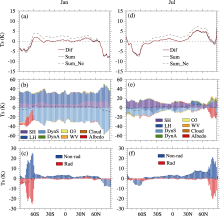
The zonal-mean T_s biases, defined as the T_s difference between FGOALS-s2 and ERA-Interim (brown curve), in January and in July are shown in Figs. 1a and 1d, respectively. It can be seen that the polar regions tend to be dominated by cold biases and the winter hemisphere is dominated by even stronger cold biases (exceeding -7 K). With regard to the colder/warmer oceanic temperature in high/low-to-middle latitudes in ERA-Interim relative to HadCRU4 (Hadley Climate Research Unit, version 4) observation data (Park et al., 2014), the model cold biases in the polar regions could be stronger compared with HadCRU4, while the model warm biases over low to middle latitudes may become smaller when compared with HadCRU4. Warm biases are found over the midlatitudes, particularly in the summer hemisphere where the maximum warm bias (~5 K) is larger than that over the tropics. To validate the decomposition by CFRAM, the sum of the partial T_s biases obtained from Eq. (5) are also shown in Figs. 1a and 1d (black solid line). It is clear that the meridional distribution, as well as the magnitude of the T_s biases, obtained through CFRAM, is almost identical to the observed T_s biases, confirming that the linearization of the radiative processes is reliable and accurate.

It should be noted that the partial temperature bias attributed to incident solar radiation at the TOA are not really model biases. It appears because the solar constant applied in FGOALS-s2 is 1365-1366 W m^-2, which is recommended by CMIP5; while that applied in ERA- Interim is 1370 W m^-2, which is estimated from multiple sources of data but has been known, on average, to overestimate the global solar radiation by about 2 W m^-2 (Dee et al., 2011). Since the partial temperature biases by individual processes in CFRAM are capable of being added linearly, we exclude the partial temperature bias solely due to the solar difference from the total temperature bias in our attribution analysis of the model biases by other physical processes. Obviously, the meridional distribution of the T_s biases does not change significantly; only the magnitudes of warm biases become relatively larger, particularly in the low-to-middle latitudes, after the partial temperature bias due to the solar difference is excluded (black dashed line vs the black solid line in Figs. 1a and 1d).

Figure 1b presents the partial T_s biases due to individual radiative and non-radiative processes in January. Generally, compared with those due to radiative processes, the magnitudes of theT_s biases due to individual non-radiative processes are remarkably lager. Specifically, larger warm biases due to the systematically overestimated downward surface sensible and latent heat fluxes are present across the winter and summer hemispheres, which are compensated for by the comparably larger cold biases due to surface dynamic processes. This suggests that, in FGOALS-s2, there may be relatively more/less energy being stored/released into the oceans/atmosphere. The magnitudes of the warm T_s biases due to atmospheric dynamics are much smaller and relatively trivial. Among the radiative processes, the cold biases due to overestimated albedo in high latitudes of the summer hemisphere are the

Figure 1

Figure Option ViewDownloadNew Window

Figure 1 (a) Boreal winter (January) zonal mean Ts biases (units: K) in terms of the difference between the Flexible Global Ocean-Atmosphere- Land System model, spectral version 2 (FGOALS-s2) and the European Center for Medium-Range Weather Forecasts (ECMWF) Re-Analysis Interim (ERA-Interim) (brown solid line), the sum of all the partial Ts biases obtained from CFRAM (black solid line), and that with the partial Ts biases due to solar difference are excluded (black dashed line). (b) Zonal mean partial Ts biases due to radiative processes including ozone, water vapor, cloud, and albedo feedback, and non-radiative processes including surface sensible and latent heat fluxes, and dynamic processes at the surface and in the atmosphere in January. (c) Zonal mean partial Ts biases due to all radiative processes (red bars) and non-radiative processes (blue bars) in January (the black dashed lines in (b, c) are the same as in (a)). Panels (d-f) are similar to (a-c), but for boreal summer (July).

strongest (up to -20 K), while the cold T_s biases in the tropics due to water vapor are related to the greenhouse effect of the underestimated water vapor content in the troposphere (Fig. 4in Yang et al., 2015). The zonal-mean T_s biases due to ozone and cloud are relatively much smaller and negligible.

The meridional distribution of the T_s biases in July is largely similar to that in January, except that the T_s biases due to surface latent heat flux in boreal summer are no longer globally positive, being negative south of 35° N with much smaller magnitudes. Accordingly, the magnitude of the cold biases due to surface dynamics is also smaller compared with that in January, suggesting smaller zonal-mean biases (or better performance) of the model in boreal summer than in boreal winter in representing the non-radiative processes that contribute to the zonal mean T_s biases.

To distinguish the relative contributions from radiative and non-radiative processes, Figs. 1c and 1f display the partial T_s biases by the two kinds of processes in January and in July, respectively. It is clear that the contributions from the radiative processes, and those from the non-radiative processes, always tend to compensate for one another, particularly over the polar region of the summer hemisphere where the cold T_s biases due to overestimated albedo are compensated for by non-radiative processes. The close compensation between radiative and non-radiative processes confirms that the coupled surface-atmosphere system always exhibits synchronized and compensatory feedbacks to energy perturbations by any physical process. Therefore, the consequent total temperature biases may not be too large, even when the model biases in representing various processes are quite large.

lists the partial T_s biases in global means. The partial T_s biases due to surface albedo, the main contributor from the radiative processes, are negative in both winter and summer, corresponding to the total radiativeT_s biases of -2.38 K and -1.92 K in January and July, respectively. Consistent with the zonal-mean distribution in Fig. 1, the total warm T_s biases due to non-radiative processes (2.76 K/3.62 K in January/July) are mainly dominated by surface heat flux processes, and are partially compensated for by surface dynamic processes in both winter and summer. Due to the compensation between radiative and non-radiative biases, the overall global mean T_s biases are much smaller (0.38 K/1.70 K in January/July), despite the relatively much larger partial biases due to each of them.

Table 1

Table 1

Table 1 Global-mean partial Ts biases (units: K) attributed to biases of partial radiative (Rad) processes including ozone (O3), water vapor (WV), cloud, and albedo feedback, and non-radiative (Non-rad) processes including surface sensible heat flux (SH) and latent heat flux (LH), and dynamic processes at the surface (DynS) and in the atmosphere (DynA). Note that the Ts biases attributed to the different incident solar radiation at the top of the atmosphere, which is not really model bias, are excluded when calculate the sum of Ts biases. Process January July Single process Sum Single process Sum Solar -1.41 -1.47 Rad O3 -0.09 -2.38* -0.11 -1.92* WV -0.35 0.10 Cloud -0.01 -0.02 Albedo -1.93 -1.89 Non-rad SH 9.70 2.76* * 10.70 3.62* * LH 23.41 -2.09 DynS -31.01 -5.61 DynA 0.66 0.62 Sum 0.38* * * 1.70* * * Note: * the sum of all the radiative processes in January and July; * * the sum of all the non-radiative processes in January and July; * * * the sum of all the radiative and non-radiative processes with the solar effect excluded in January and July.

Table 1 Global-mean partial Ts biases (units: K) attributed to biases of partial radiative (Rad) processes including ozone (O3), water vapor (WV), cloud, and albedo feedback, and non-radiative (Non-rad) processes including surface sensible heat flux (SH) and latent heat flux (LH), and dynamic processes at the surface (DynS) and in the atmosphere (DynA). Note that the Ts biases attributed to the different incident solar radiation at the top of the atmosphere, which is not really model bias, are excluded when calculate the sum of Ts biases.

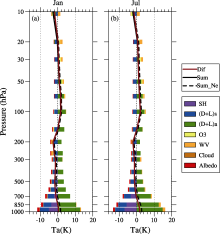
Similar to the T_s biases, we first validate that the observed global-mean T_a biases (brown curve in Fig. 2) are highly consistent with the sum of partial T_a biases obtained through CFRAM (black solid curve in Fig. 2). They both exhibit warm biases in the lower troposphere and lower stratosphere, and cold biases in the mid-to- upper troposphere and upper stratosphere, in boreal winter as well as in boreal summer. Furthermore, the total T_a biases when the partial T_a biases due to a shortage of solar radiation are excluded (black dashed line in Fig. 2), also exhibit a similar vertical distribution, albeit with the amplitudes of the warm/cold biases being slightly larger/ smaller.

Note that, unlike the effects of surface sensible heat flux on the atmosphere, which can be obtained directly, the heating rate of the surface latent heat flux in the atmospheric layer is usually unavailable in both model results and reanalysis data; the energy perturbation by surface latent heat flux (L) in CFRAM is considered as part of that by dynamical processes (D). For ease of reference, we use and to represent their combined contributions in the atmosphere and at surface, respectively.

Figure 2

Figure Option ViewDownloadNew Window

Figure 2 Vertical profiles of the global-mean partial Ta biases (units: K) due to radiative processes and non-radiative processes (bars), the sum of all the partial Ta biases obtained from CFRAM (black solid line), that with the partial Ta biases due to solar difference excluded (black dashed line), and the Ta biases in terms of the difference between FGOALS-s2 and ERA-Interim (brown line) in (a) January and (b) July.

It can be seen from Fig. 2 that the vertical distributions of most of the global mean partial T_a biases due to individual processes are highly similar between January and July. The magnitudes of the total T_a biases are around ± 3 K at most, while those of the individual processes are up to ± 10 K— much larger than the T_a biases we observed. This again indicates the synchronized and compensatory feedbacks to energy perturbations by any physical process within the coupled surface-atmosphere energy balance system. Specifically, the exhibit warm biases from the surface layer to 50 hPa, with the maximum exceeding 14 K near the surface, which are mainly compensated for by from the mid-troposphere to lower-stratosphere, and are compensated for by both and surface sensible heat flux in the lower troposphere. Similar to the T_s biases, the magnitudes of the partial T_a biases due to individual radiative processes are relatively smaller than those due to individual non-radiative processes. The cold biases due to surface albedo are seen throughout the atmospheric layers, which is associated with the reduction of longwave radiation from the surface due to the cold T_s biases caused by the overestimated surface albedo. The warm T_a biases due to ozone process are confined to the stratosphere, reflecting the effect of the increased absorption of shortwave radiation by the greater ozone amount in the model. Associated with the smaller water vapor amount in the model stratosphere (Ren et al., 2015), the warm biases there are mainly a result of the reduced outgoing longwave radiation. The global-mean T_a biases due to bias in cloud are negligible, as are the partial T_s biases.

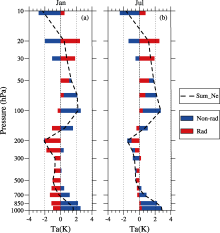
To further quantify the relative contributions to the T_a biases, the global-mean T_a biases due to all radiative (except solar radiation) and all non-radiative processes are shown in Fig. 3. Despite the small amplitudes of the partial T_a biases by individual radiative processes, their overall contributions to the total T_a biases are comparable to those by the non-radiative processes. In the surface layer, the total warm biases (dashed line) are mainly dominated by non-radiative processes, and are compensated for by the cold biases due to radiative processes. In the mid-to-upper troposphere from 700 to 200 hPa, the radiative processes are overwhelming. In the stratosphere, biases are mostly dominated by non-radiative processes, except in the mid-stratosphere where ozone feedback largely dominates.