Various ensemble-based schemes are employed in data assimilation because they can use the ensemble to estimate the flow-dependent background error covariance. The most common way to generate the real-time ensemble is to use an ensemble forecast; however, this is very time-consuming. The historical sampling approach is an alternative way to generate the ensemble, by picking some snapshots from historical forecast series. With this approach, many ensemble-based assimilation schemes can be used in a deterministic forecast environment. Furthermore, considering the time that it saves, the method has the potential for operational application. However, the historical sampling approach carries with it a special kind of sampling error because, in a historical forecast, the way to integrate the ensemble members is different from the way to integrate the initial conditions at the analysis time (i.e., forcing and lateral boundary condition differences, and ‘warm start’ or ‘cold start’ differences). This study analyzes the results of an experiment with the Global Regional Assimilation Prediction System-Global Forecast System (GRAPES-GFS), to evaluate how the different integration configurations influence the historical sampling error for global models. The results show that the sampling error is dominated by diurnal cycle patterns as a result of the radiance forcing difference. Although the RMSEs of the sampling error are small, in view of the correlation coefficients of the perturbed ensemble, the sampling error for some variables on some levels (e.g., low-level temperature and humidity, stratospheric temperature and geopotential height and humidity), is non-negligible. The results suggest some caution must be applied, and advice taken, when using the historical sampling approach.
A large number of ensemble-based data assimilation schemes have been developed to date, including both ensemble filter schemes (Evensen, 1994; Hunt et al., 2007) and ensemble variational schemes (Liu et al., 2008; Tian et al., 2008, 2011; Wang et al., 2010). The ensemble in these schemes plays an important role in estimating the flow-dependent background error covariance (BEC) and thus ensures the analysis increment is more consistent with the real-time atmospheric dynamics. In most cases, the ensemble is generated by a separate or coupled ensemble forecast system. However, the ensemble forecast is computationally very expensive and not all research groups or operational centers can afford it. Even for those with an ensemble forecast system, the ensemble number is always limited to less than 100 due to the high computational cost.
The historical sampling approach is a new approach, proposed by Wang et al. (2010), along with a new ensemble-variational scheme named Dimension-Reduced Projection 4DVar (DRP-4DVar). This sampling approach generates the ensemble by picking some snapshots from recent historical forecast series and thus maintains the flow dependency while avoiding the need for an ensemble forecast. In numerical weather prediction centers, this approach demands almost no computational cost, as historical forecast series are already available in operational systems. Another advantage of this approach is that the ensemble number can be much larger (limited only by the length of historical forecast series). With this historical sampling approach, many ensemble-based assimilation schemes can be used in a deterministic prediction environment. Currently, there are several assimilation applications using this historical sampling approach (Wang et al., 2010, 2011; Tian et al., 2011; Zhao et al., 2012).
However, as an empirical method, there is no theoretical guarantee as to how the ensemble generated by the historical sampling approach represents the atmospheric background error distribution. As noted by Zhao and Wang (2010), its ensemble spread is often too small, though this can be alleviated by inflating the BEC or increasing the sampling time interval between adjacent historical samples. Besides, as noted later in the paper, when used for 4D ensemble-based schemes, the historical sampling approach carries with it a special kind of sampling error, caused by the inaccurate integration configurations of the historical ensemble members. The problem of this sampling error has not yet been addressed, and so both its magnitude and distribution pattern are still unknown. In this paper, we provide a detailed description of this special sampling error, and then evaluate it with the Global Regional Assimilation Prediction System-Global Forecast System (GRAPES-GFS).
The organization of the remainder of the paper is as follows. The historical sampling approach is described in section 2. The experimental design and results are given in section 3. Finally, a summary and discussion are provided in section 4.
To exemplify how the historical sampling approach works for ensemble-based data assimilation schemes, a brief introduction to DRP-4DVar is given first.
DRP-4DVar is one of the representative 4D ensemble-variational assimilation schemes (Wang et al., 2010). In DRP-4DVar, we first need to prepare the perturbed model space ensemble Px and its projection onto the observation space, as follows:
To exemplify how the historical sampling approach works for ensemble-based data assimilation schemes, a brief introduction to DRP-4DVar is given first.
DRP-4DVar is one of the representative 4D ensemble-variational assimilation schemes (Wang et al., 2010). In DRP-4DVar, we first need to prepare the perturbed model space ensemble Px and its projection onto the observation space, as follows:
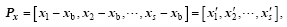 (1)
(1)
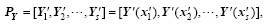 (2)
(2)
where xb is the background and s is the ensemble size. Each member (column) of Px represents the 3D model state increment (relative to the background xb) in the beginning of the assimilation window, while each member (column) of PY represents the simulated observation increment (relative to the background simulated observation Yb=Y(xb)) within the whole window. Y(x), ‘ the observation simulator’ , consists of the forecast model and the observation operator, i.e., 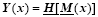
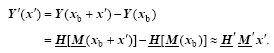 (3)
(3)
The underlined letters 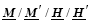
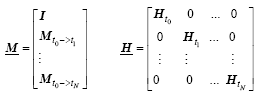
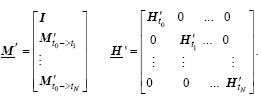 (4)
(4)
The letter I represents the unit matrix. The operator 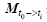

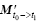

As shown in Eq. (3), an approximate linear relationship between Px and PY exists; thus, for the model space increment expressed as
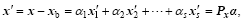 (5)
(5)
its simulated observation increment is approximated linearly in the vicinity of xb as
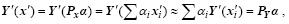 , (6)
, (6)
where 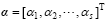
Thus, x’ and Y’ (x’ ) are replaced by linear operators (Pxa, Pya, respectively). In this way, the DRP-4DVar cost function is an explicit quadratic function of a, as follows:
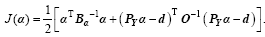 (7)
(7)
In Eq. (7), Bais the BEC matrix with respect to a, O is the observation error covariance, and d is the innovation (observation minus background simulated observation). From the brief review above, the ensemble not only estimates the BEC, but also approximates Y’ (x’ ). So, it is inferred that the quality of the ensemble (Px, PY) is crucial to the performance of DRP-4DVar. A simple flowchart of DRP-4DVar is given in Fig. 1a.
Note that in this work, for simplicity, we assume that the analysis time is in the beginning of the window; however, it can be tuned within the whole window for DRP-4DVar, as well as many other 4D ensemble-based methods (Liu et al., 2009; Zhao et al., 2011; Wang et al., 2011). Readers are referred to Wang et al. (2010) and Shen et al. (2014) for the detailed derivation of DRP- 4DVar.
As seen in the last section, DRP-4DVar, as well as many other ensemble-based schemes, needs to prepare the ensemble before minimization. Generally, an ensemble forecast is used to generate the ensemble at the analysis time by integrating the analysis ensemble of the last assimilation, i.e., through the ensemble cycling assimilation. Besides, for those 4D ensemble-based schemes that assimilate observations within the whole window, an extra ensemble forecast integration is needed to generate the observation space ensemble, i.e., Py=Y’ (Px). Thus, two ensemble forecast integrations are needed in each window. As a result, huge computational cost is expected.
The historical sampling approach is an alternative way to generate the ensemble much more efficiently. Wang et al. (2010) gave an example of how this sampling approach can be operated. In this example, two 78-h continuous forecasts with one output per hour are prepared, which are initialized with certain analysis data at 24 h and 48 h earlier than the beginning of the window, respectively. Figure 1b demonstrates the example of the sampling process for one historical series. Considering the assimilation window of 6 h, each 78-h forecast series contains 73 windows with each window shifted 1 h from another. So, 73 members are picked for each forecast series and a total of 146 members are obtained. As shown in Fig. 1b, the model space ensemble {xi(to)} is obtained directly from the 1-h output of the model, while the observation space ensemble 
 (8)
(8)
Thus, once the historical forecast series is prepared, no model integration is needed to generate the ensemble. Given the analysis-time background xb and its projection on observation space Yb, the perturbed ensemble members (i.e., members of Px/PY) are calculated by subtracting the background from each member:
 (9)
(9)
Although the historical sampling approach has many advantages, there is one potential problem associated with this method. As shown in Figs. 1b and 1c, unlike the ensemble forecast sampling approach, the integration intervals for historical ensemble members are shifted away from the assimilation window (00-06). As a result, the forcing (including sea surface temperature) and the lateral boundary condition (only for regional models) are different to that in the integration within the assimilation window. In fact, from Eq. (8), the underlying assumption for the historical sampling approach is that the prediction problem is an initial-value problem, where the forecast results are totally determined by the initial condition (IC). Besides, as the historical forecast series is a continuous run, the historical ensemble can be seen as generated by warm-start integrations, while in reality the ICs should be integrated in a cold-start way. As a consequence, these inaccurate integration configurations of the historical ensemble will probably introduce a special kind of sampling error for 
As shown in Fig. 1c, we can conduct an ensemble forecast in the correct configuration and initialized with the ensemble {xi(to)} generated by the historical sampling approach. If the historical sampling approach has no such sampling error, its observation space ensemble 
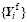


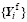
GRAPES-GFS (Zhang and Shen, 2008) is a global weather forecast system based on the GRAPES model, which is developed by the China Meteorological Administration. In this study, the GRAPES-GFS with a 1° resolution, 36 vertical levels, and 600-s time step configuration is utilized. Besides, the code is modified so that during the integration it outputs the input-file-formatted files every hour, which can be used directly as the initial input files for GRAPES-GFS.
Initialized with the 1° × 1° resolution National Centers for Environment Prediction final global tropospheric (NCEP/FNL) analysis, a 78-h integration starting from 0000 UTC 1 June 2011 provides a historical forecast series for the analysis at 0000 UTC 3 June 2011. Seventy-three ensemble members ({xi(to)}) are picked, and then each is used as the IC to start a 6-h integration from 0000 UTC 3 June 2011, to generate the reference ensemble 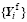
Here, it is assumed that the observations are measured directly on every grid point, so, in fact, no observation operators are performed. Furthermore, for additional simplicity, we assume the observations are at the end of the window. So, we just need to compare the terminal output of the model to begin with, but we then show the impact of the observations at different times at the end of section 3.2.
Using 
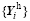
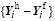
Besides the radiance forcing, the impact of the ‘ cold-start or warm-start’ integration difference can also be observed. From Figs. 2b-e, the -48-h shifted historical ensemble member has even smaller sampling errors than that of the 00-h shifted member. We speculate that the reason is that the -48-h shifted historical ensemble member is integrated in a ‘ cold-start’ configuration, the same as that of the reference, while the 00-h shifted historical ensemble member is integrated in the different ‘ warm- start’ configuration.
Although the evidence of the two sources of sampling error is clear, their magnitudes are very small, which suggests the 6-h integration can be approximated as an initial-value problem. However, it cannot be simply concluded that the historical sampling error is negligible. Actually, as shown in Eq. (7), it is the perturbed ensemble, rather than the original ensemble, that matters in the assimilation. So, we recalculate the correlation coefficients between the perturbed ensemble 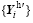
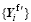

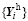
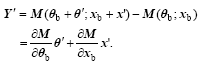 (10)
(10)
From Eq. (10), the perturbed forecast Y’ consists of two items, one caused by the perturbed forcing 
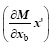
 (11)
(11)
For the historical ensemble members sampled during the second and third cycles, as their times are closer to the analysis time compared to the first cycle, they are more likely to have smaller perturbed ICs ( 

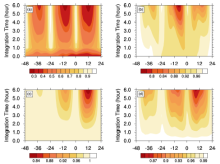
From the vertical distributions of the sampling error (PCOR shown in Fig. 3), besides the low level temperature, the stratospheric temperature is also perturbed in a diurnal cycle pattern, which can be attributed to the high concentration of ozone in the stratosphere. Influenced through the hydrostatic balance relationship, the high level geopotential height also shows a significant diurnal cycle pattern. For the specific humidity, many small- scaled large-negative-valued correlation noises exist above 100 hPa, especially around the 20 hPa level. However, we are unsure whether this small-scaled structure is model-dependent or physically reasonable. For the low level humidity (lower than 900 hPa), its sampling error also has a typical diurnal cycle pattern, with its minimum PCOR at around 0.8 (unrecognized in Fig. 3c). Unlike these three thermal variables, the zonal wind suffers only slightly from the sampling error.
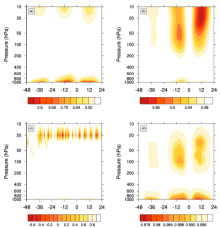 | Figure 3 Vertical distributions of historical sampling errors (PCOR) for (a) temperature, (b) geopotential height, (c) specific humidity, and (d) zonal wind. |
Until now, all the comparisons have been performed under the assumption that the observations are at the terminal end of the window. In Fig. 4, we give a simple demonstration of how the observation time influences the sampling errors. As expected, as the integration time increases, the forcing’ s contribution to the forecast results enlarges and the magnitudes of the sampling errors are amplified. These results suggest that the sampling error can be alleviated if a shorter assimilation window is selected or the analysis time is set in the middle of the window.
The historical sampling approach provides a very efficient way to generate ensemble members for data assimilation without conducting an ensemble forecast. In this paper, we point out one potential problem associated with this approach when used for 4D ensemble-based schemes, which may introduce a special kind of sampling error for the observation space ensemble 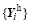
From the results, we can propose some simple advice for the historical sampling approach, when used with 4D ensemble-based schemes. For example, to skip sampling at some specific sampling time, to exclude some observations sensitive to some specific variables on some specific levels, to use a shorter window, or to set the analysis time in the middle of the window. Besides, we may also develop some bias correction schemes based on the diurnal cycle characteristics. As this work is only a simple evaluation, other questions as to how this sampling error affects the assimilation and how to overcome this sampling error still need further investigation. In addition, the sampling error for regional models is another important question, where the lateral boundary conditions may play a more important role, and thus the sampling error is probably even larger. Finally, more research on other aspects of the historical sampling approach, e.g., the representativeness of the historical ensemble, and elaborative tuning of the sampling process, is also necessary before this approach can be applied operationally.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|