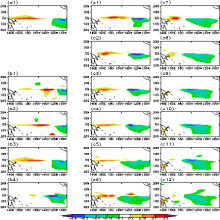
Based on the Zebiak-Cane model, the time- dep-endent nonlinear forcing singular vector (NFSV)-type tendency errors with components of 4 and 12 (denoted by NFSV-4 and NFSV-12) are calculated for predetermined El Niño events and compared with the constant NFSV (denoted by NFSV-1) from their patterns and resultant prediction errors. Specifically, NFSV-1 has a zonal dipolar sea surface temperature anomaly (SSTA) pattern with negative anomalies in the equatorial eastern Pacific and positive anomalies in the equatorial central-western Pacific. Although the first few components in NFSV-4 and NFSV-12 present patterns similar to NFSV-1, they tend to extend their dipoles farther westward; meanwhile, the posi-tive anomalies gradually cover much smaller regions with the lag times. In addition, the authors calculate the prediction errors caused by the three kinds of NFSVs, and the results indicate that the prediction error induced by NFSV-12 is the largest, followed by the NFSV-4. However, when compared with the prediction errors caused by random tendency errors, the NFSVs generate significantly larger prediction errors. It is therefore shown that the spatial structure of tendency errors is important for producing large prediction errors. Furthermore, in exploring the tendency errors that cause the largest prediction error for El Niño events, the time-dependent NFSV should be evaluated.
Citation: Zhao, P., and W.-S. Duan, 2014: Time-depen-dent nonlinear forcing singular vector-type tendency error of the Zebiak-Cane model, Atmos. Oceanic Sci. Lett., 7, 395-399, doi:.
In realistic ENSO predictions, the prediction errors are generally caused by initial errors and model errors. Many studies have explored the effect of initial errors on ENSO predictability and emphasized the important role of initial errors in a successful ENSO forecast ( Chen et al., 2004; Mu et al., 2007a, b; Duan et al., 2009). Recently, increasing numbers of scientists have paid attention to the predictability of ENSO associated with model error ( Wu et al., 1993; Hao and Ghil, 1994; Blanke et al., 1997; Flügel and Chang, 1998; Latif et al., 1998; Liu, 2002; Zhang et al., 2003; Zavala-Garay et al., 2004; Williams, 2005). The model errors may arise from various schemes of physical parameterizations ( Syu and Neelin, 2000), atmospheric noise, or other high-frequency variations such as westerly wind bursts and the Madden-Julian oscillation ( Gebbie et al., 2007; Tang and Yu, 2008; Marshall et al., 2009). Considering the effect of uncertainties in empirical model parameters on ENSO predictability ( Mu et al., 2002), Duan and Zhang (2010) and Yu et al. (2012) used an approach of conditional nonlinear optimal perturbation (CNOP) to explore the influence of model parametric errors on ENSO predictability and argued that the parameter errors may have less influence on prediction uncertainties of ENSO. Model parameter error is only one source of model errors and cannot represent all types of model errors. Further-more, we cannot separate exactly the effect of each type of model error from prediction uncertainties. Therefore, it is challenging to explore the effect of model errors using the approach used in Duan and Zhang (2010).
Duan and Zhao (2014) used the nonlinear forcing sing-ular vector (NFSV) approach to study the effect of tendency errors on prediction uncertainties, where the tend-ency errors are described by an constant external forcing and attempt to represent the effect of all types of model errors on prediction uncertainties. However, the NFSV used in Duan and Zhao (2014)¢Ù is time-independent and cannot reveal the effect of time-dependent tendency errors on prediction uncertainties. That is to say, the constant NFSV may be limited in describing the optimal tendency errors. In this paper, we study the time-dependent NFSV and reveal the difference between constant NFSV and time-dependent NFSV based on the Zebiak-Cane model ( Zebiak and Cane, 1987).
The NFSV is a tendency perturbation that satisfies a given constraint and has the largest nonlinear evolution at the prediction time ( Duan and Zhou, 2013). The NFSV approach is a natural generalization of the forcing singular vector ( FSV; Barkmeijer et al., 2003) approach to nonlinear fields.
For an appropriate measurement
| (1) |
where
| (2) |
where
The time-dependent NFSVs represent the tendency errors that cause the largest prediction error for a lead time, which is probably caused by the uncertainties of various schemes of physical parameterizations, atmospheric noise, or other high-frequency variations such as westerly wind bursts and the Madden-Julian oscillation, or their combinations. Here, we simply use a norm
The Zebiak-Cane model ( Zebiak and Cane, 1987) was the first coupled model of intermediate complexity to simulate the observed ENSO inter-annual variability. It became well known for successfully predicting the 1991/1992 El Niño event. The Zebiak-Cane model has been widely used in ENSO prediction and predictability research ( Blumenthal, 1991; Xue et al., 1994; Chen et al., 2004; Tang et al., 2008; Mu et al., 2007a; Duan et al., 2012; Yu et al., 2012) and is a useful platform for studying ENSO predictability.
To explore the effect of tendency errors on ENSO prediction uncertainties using the NFSV approach, we first construct the corresponding cost function according to Eqs. (1) and (2):
| (3) |
where
The reference states used here are the El Niño events obtained by integrating the Zebiak-Cane model with the CNOP-type initial anomalies (see Mu et al. (2003) for details) shown in Fig. 1. These two initial anomalies evolve into a weak El Niño and a strong El Niño (denoted by Ref-1 and Ref-2; see Fig. 2), respectively (for more details, refer to Duan et al. (2012)).
In this context, for the two El Niño events, we make predictions for 12 months starting in January. To obtain the NFSVs, we determine experimentally the constraint radiuses
 | Figure 2 Niño-3 index of the El Niño events induced by the CNOP-type initial anomalies shown in Fig. 1, which are a weak El Niño event and a strong El Niño event (denoted by Ref-1 and Ref-2). |
Figure 3 plots the patterns of the three kinds of NFSVs of Ref-1. It is shown that NFSV-1 has a zonal dipolar SSTA pattern with negative anomalies in the equatorial eastern Pacific and positive anomalies in the equatorial central-western Pacific (see Fig. 3a1). Although each com-ponent of NFSV-4 and NFSV-12 tends to have a large- scale dipole pattern similar to NFSV-1, there are differences. To be specific, the first few components of NFSV-4 and NFSV-12 tend to present a westward-moving trend of their dipoles with the lag time; furthermore, the positive anomalies in the patterns gradually become weak. It is obvious that there are differences between NFSV and time-dependent NFSV. Furthermore, we find that the time-dependent NFSV causes much large prediction errors compared to the constant NFSV (see next section) and shows itself to be better at revealing the tendency errors that cause the largest prediction error. Therefore, if we consider the optimal tendency errors, we should explore the time-dependent NFSV.
We also obtain similar results for Ref-2. That is to say, the spatial structure of the NFSVs, whether they are constant or time-dependent, have similar patterns to those in Fig. 3. It is indicated that the large-scale patterns of the NFSVs may be independent of the intensity of the El Niño events.
After exploring the features of the spatial structure of the three kinds of NFSVs for Ref-1, we subsequently study the prediction errors that they induce. In this experiment, we consider the prediction errors of a tropical Pacific SSTA field described by the Zebiak-Cane model (see section 3) and use the
In addition, we also estimate the prediction errors caused by the NFSVs for Ref-2 and obtain similar results (see Table 1), which also demonstrates the importance of the spatial structure of tendency errors in yielding significant prediction errors and emphasizes the optimality of time-dependent NFSV.
In this article, based on the Zebiak-Cane model of intermediate complexity, we explore the time-dependent NFSVs of two El Niño events with different intensities, where the El Niño events are obtained by integrating the CNOP-type initial anomalies with an initial time of January and initial constraint radiuses of 0.4 and 1.0, which correspond to a weak and a strong El Niño, respectively. For comparison, we also compute the constant NFSV of these two El Niño events. The constant NFSVs and time- dependent NFSVs are both calculated for an optimization period of 12 months. The results demonstrate that the constant NFSVs tend to possess a zonal dipolar SSTA pattern with negative anomalies in the equatorial eastern Pacific and positive anomalies in the equatorial central- western Pacific. We calculate the time-dependent NFSVs with the optimization time period divided into continuous four and twelve equivalent time intervals. The results indicate that although the first few components of NFSV-4 and NFSV-12 have dipole patterns similar to NFSV-1, there are differences in them. To be specific, the first few components of NFSV-4 and NFSV-12 tend to present a westward-moving trend of their dipoles with the lag time interval; furthermore, the positive anomalies in the patterns gradually become much weaker. In addition, we exp-lore the prediction errors generated by NFSV-1, NFSV-4, and NFSV-12 for Ref-1 and Ref-2. Results show that the time-dependent NFSV causes larger prediction errors com-pared to the constant NFSV. Specifically, among the predi-ction errors caused by the three kinds of NFSVs, NFSV-12 induces the biggest prediction error, followed by NFSV-4, and finally NFSV-1, namely the constant NFSV, causes the smallest prediction error. Nevertheless, comparing with the random tendency error, both time-dependent and time-independent NFSV can cause more significant prediction errors. All these results suggest that a particular spatial structure of NFSVs plays an important role in tendency errors causing large prediction errors. Moreover, the time-dependent NFSV, compared to the constant NFSV, is more applicable in describing the optimal tendency errors that cause the largest prediction errors.
| Table 1 Prediction errors caused by the nonlinear forcing singular vector (NFSV)-type and random tendency errors. |
It is noted that the NFSVs obtained in the present paper have patterns similar to those of the CNOP-type initial errors. In particular, both of them concentrate the errors in the same region: equatorial central-eastern Pacific Ocean, which may suggest that the prediction errors generated by the Zebiak-Cane model may be sensitive not only to the initial errors but also to the tendency errors in this region. Therefore, if we increase the observations in this region, we can not only improve the initial fields but also correct the model by assimilating these additional observations, finally greatly improving the forecast skill of El Niño events.
The integration time step of the Zebiak-Cane model is 10 days. Theoretically, if the time-dependent NFSV is computed at each time step, it may cause much larger pred-iction errors than NFSV-4 and NFSV-12. The time-depen-dent NFSV related to each time step may increase the degrees of freedom and become time consuming; furthermore, such time-dependent NFSVs may have patterns that do not satisfy the physics. Actually, for the time-dep-endent NFSV related to each time step, the tendency perturbation at each time step may not have enough time to include the atmospheric and oceanic variables feedback from each other, which means that the time-dependent NFSV related to the time step is unphysical. So, in the present study, we compute the time-dependent NFSV related to each month or each season, which may guarantee having enough time for the atmospheric and oceanic variables to feedback to each other.
It should be pointed out that, when calculating the time-dependent NFSV in the present paper, the gradient of the cost function required by the NFSV calculation is directly computed according to the definition of gradient, which is not the same as calculating the constant NFSV using the adjoint method. The former is more time-consu-ming and may be difficult to apply in complex GCMs. Furthermore, there is not yet a fast algorithm to deal with the calculation of the 'time-dependent' NFSV with many more degrees of freedom. Therefore, a highly effective algorithm should be developed to solve the time-dependent NFSV in future work. As expected, by the effective cooperation of computation mathematicians and meteorologists the time-dependent NFSV can be successfully applied in more complex models and play an important role in revealing the optimal tendency errors in the future.
Acknowledgements. The authors appreciate the insightful comments and suggestions of the two anonymous reviewers. This work was jointly sponsored by the National Basic Research Program of China (Grant No. 2012CB955202), the National Public Benefit (Met-eorology) Research Foundation of China (Grant No. GYHY2013-06018), and the National Natural Science Foundation of China (Grant Nos. 41176013 and 41230420).
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|