Taking into account moisture in virtue of general potential temperature, the author derive a three-dimensional (3D) pseudomomentum wave-activity relation for the moist atmosphere from the primitive equations in Cartesian coordinates using the Momentum-Casimir method. Since the wave-activity relation is constructed in an ageostrophic and non-hydrostatic dynamical framework, it may be applicable to diagnosing the evolution and propagation of mesoscale systems leading to heavy rainfall. The theoretical analysis shows that, besides the local change of wave-activity flux divergence and source or sink, the wave-activity relation includes two additional forcing terms. The first is the zonal gradient of difference between general potential temperature and potential temperature perturbations, and the second is the covariance of the solenoid and gradient of water vapor, denoting the direct influence of moisture on wave-activity density.
The wave-activity density was applied to a heavy precipitation event occurring in the Jianghuai region of China. The calculation showed that the wave-activity density was consistent with 6-h accumulated precipitation observations, in terms of both spatial distribution and temporal tendency. This suggested that the disturbance represented by wave-activity density was closely related to the heavy precipitation. Although the wave-activity flux divergence and the covariance of the solenoid and gradient of water vapor made the primary contribution to the local change of wave-activity density, the covariance was more remarkable. The zonal gradient of difference between general potential temperature and potential temperature perturbations made a weaker contribution to the wave- activity density.
A variable can be decomposed into a basic state and a disturbance, which is generally called a “wave” or “vortex”. The interaction between a basic state and disturbance is called the wave-flow interaction. Some weather phenomena can be explained by the theories of wave-flow interaction. For example, the theory of upward propagation and breakdown of a gravitational wave can interpret the quasi-biennial oscillation between easterly and westerly wind in the equatorial stratosphere ( Lindzen and Holton, 1968). Furthermore, the explosive warming of the stratosphere can be interpreted by the critical layer theory of planetary waves ( Matsuno, 1970), and the acceleration and deceleration phenomena of the upper-level jet stream can be illustrated by Eliassen-Palm flux (EPF) theory ( Gao and Tao, 1990; Gao et al., 2004b; Pfeffer, 1992).
Research on wave-flow interaction includes two aspects: (i) EPF theory presenting the feedback of waves on basic-sate flow ( Andrews, 1983); and (ii) the “wave- activity” (conservation) equation describing the forcing of basic-state flow to waves ( Brunet et al., 1996; Durran, 1995; Magnusdottir and Haynes, 1996; Mu et al., 1999; Mu, 1998; Murray, 1998). Zeng (1986) pointed out that the non-zonal disturbance is completely absorbed by the zonal flow and the absorption relies on cuts of the zonal jet stream and disturbance scales. Zeng and Zhang (2000) found that the continuous spectrum plays an influential role in wave-flow interaction. Huang et al. (1983) and Huang and Gambo (1983) proposed the propagation theory of planetary waves in a three-dimensional (3D) spherical surface atmosphere. Wu and Chen (1989) further generated the EPF in a moist atmosphere. Lu (1995) deduced the conservation equations of Rossby wave momentum by using the WKB (Wentzel-Kramers-Brillouin) approximation method. Ding and Shen (1998) introduced EPF theory into the dynamic model of mesoscale symmetrical disturbance.
Scinocca and Shepherd (1992) and Haynes (1988) defined the “wave-activity density” as a disturbance quantity that is quadric or higher-order in disturbance amplitude in the small-amplitude limit. It satisfies the wave- activity relation in a flux form
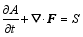 | , (1) |
where A is the wave-activity density (naturally, it represents a kind of wave energy), F is the wave-activity flux, and S is the source or sink of wave-activity density. Both A and F are the quadric or higher-order terms in disturbance fields. McIntyre and Shepherd (1987) and Haynes (1988) proposed the Momentum-Casimir method to derive the wave-activity relation. Ran and Gao (2007) and Ran and Boyd (2008) established the pseudomomentum wave-activity relation suitable for mesoscale systems.
Most previous studies have focused on the wave-flow interaction of large-scale systems under the conditions of quasi-geostrophic approximation and hydrostatic balance. Moisture has not been taken into account in earlier work, with investigations into wave-flow interaction of ageostrophic and non-hydrostatic mesoscale systems in a moist atmosphere being few in number. In this context, the present paper aims to investigate the ageostrophic and non- hydrostatic pseudomomentum wave-activity relation for the moist atmosphere and apply it to a precipitation event. In the next section, the moist wave-activity relation is derived. In section 3, the wave-activity relation is applied to diagnosing a precipitation event. And finally, a summary of the findings is provided in section 4.
For a diabatic and frictionless moist atmosphere, the governing equations in the Cartesian coordinates on the f plane are given by
 | , (2) |
 | , (3) |
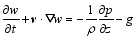 | , (4) |
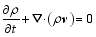 | , (5) |
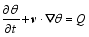 | , (6) |
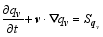 | , (7) |
 | , (8) |
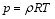 | , (9) |
Here, v = ( u, v, w) is the 3D velocity vector, ρ is the density, g is the accelerarion of gravity, θ is the potential temperature, T is the temperature, qv is the specific humidity, Q is the diabatic heating, Sqv is the source or sink of qv, ps is the pressure of the reference level, R is the dry air gas constant, and Cp is the specific heat at constant pressure.
The general potential temperature can be described by ( Gao et al., 2004a)
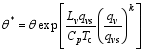 | , (10) |
where Lv is the latent heat, Tc is the temperature at the condensation lift level, qvs is the specific humidity of sat-
urated moisture and k is the empirical constant. By using Eqs. (6) and (10), one can obtain the equation of θ* as
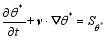 | , (11) |
where
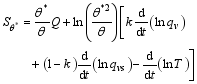
is the source or sink.
With Eqs. (2), (3) and (11), one has
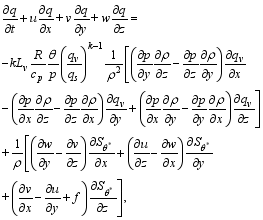 | (12) |
where 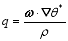
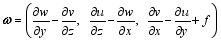
Combining Eqs. (2) and (5) yields
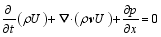 | , (13) |
where U = u - fy is the absolute zonal momentum.
A Casimir function is defined as a single-value function of moist potential vorticity and general potential temperature; namely, C = C( q, θ*). It satisfies
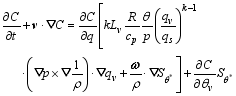 | , (14) |
Summing Eqs. (13) and (14) yields
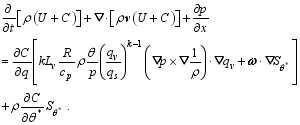 | , (15) |
This equation will be used to derive the moist wave- activity relation suitable for a mesoscale system.
A variable is assumed to be decomposed to a basic state and a disturbance:
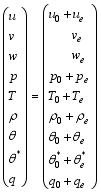 | , (16) |
Here, subscripts “0” and “ e” denote the basic state and the disturbance, respectively. The basic-state generalized potential temperature is a function of z, and the other basic states are functions of y and z. The basic states are subjected to the following relations:
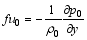 | , (17) |
 | , (18) |
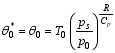 | , (19) |
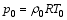 | , (20) |
Taking the Tyler series expansion of C = C( q, θ*) at ( q0, 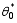
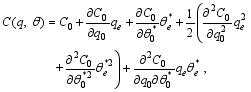 | , (21) |
where C0 = C0( q0, 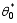
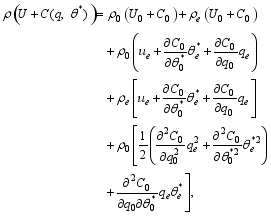 | (22) |
where U0 = u0 - fyis the basic-state absolute momentum. The potential vorticity perturbation is given by
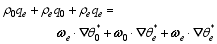 | , (23) |
where 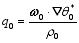
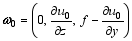
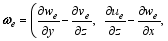
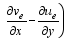
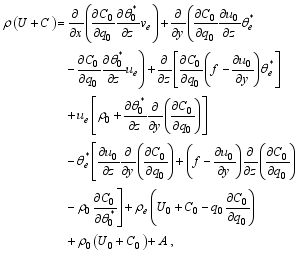 | , (24) |
where
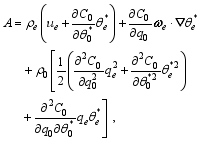 | (25) |
is the so-called moist pseudomomentum wave-activity density (wave-activity density, for short), which is quadric in disturbance fields.
According to the Momentum-Casimir method, in order to rewrite the right-hand side of Eq. (25) as the sum of leading-order flux divergence and A, we choose C0 to satisfy
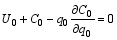 | , (26) |
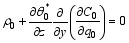 | , (27) |
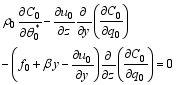 | , (28) |
where 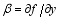
It can be proven that, if Eq. (26) holds, then Eqs. (27) and (28) are automatically satisfied. This suggests that Eqs. (26)-(28)are intrinsically equivalent. From Eq. (27), one has:
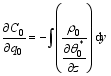 | , (29) |
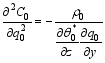 | , (30) |
In virtue of Eqs. (26) and (28), one obtains:
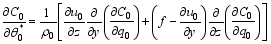 | , (31) |
 | , (32) |
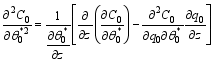 | , (33) |
For the known basic states, 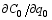
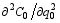
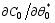
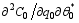
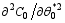
With Eqs. (26)-(28), one can rewrite Eq. (24) as
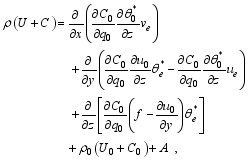 | (34) |
or
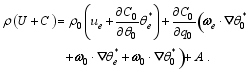 | (35) |
Substituting Eqs. (24) and (35) into the first and second terms on the left-hand side of Eq. (15), respectively, and then substituting Eqs. (17)-(20) and (26)-(28), one obtains the moist wave-activity relation
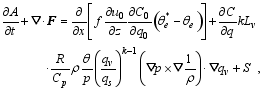 | (36) |
where
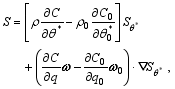 | (37) |
is the source or sink of A, and F = ( Fx, Fy, Fz) is the wave- activity flux quadric in disturbance fields with the components
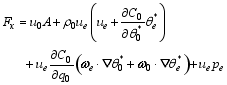 | , (38) |
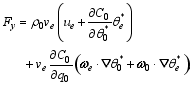 | (39) |
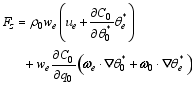 | , (40) |
Different from the general form of the wave-activity relation (Eq. (1)), Eq. (36) contains the two additional forcing terms. The first term on the right-hand side of Eq. (36) represents the zonal gradient of difference between general potential temperature and potential temperature perturbations. The second term on the right-hand side of Eq. (26) represents the covariance of the solenoid and gradient of water vapor.
For a closed system with periodic boundaries, the volume integration of moist wave-activity density is not conserved. It is dominated by the covariance of the solenoid and gradient of water vapor, and the source or sink; namely,
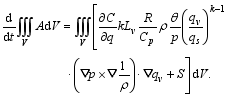 | , (41) |
When the moist atmosphere is saturated, qv = qvs( p, T), so that the covariance disappears. For dry air, the covariance vanishes.
Involving moisture in the ageostrophic and nonhydrostatic framework, the moist wave-activity relation is capable of describing mesoscale perturbation. In the following section, the moist wave-activity density and wave- activity flux divergence are diagnosed in a heavy precipitation event.
A heavy precipitation event occurred in East China between 0000 UTC 17 July 2007 and 0000 UTC 21 July 2007, leading to severe flash flooding in Shandong Province, and with maximum rainfall reaching 153.1 mm in Jinan City. This extreme event was caused by the interaction of the westerly trough, lower-level shear line, and subtropical high. The transportation of warm-moist air by the lower-level southwestern jet provided favorable thermal conditions and adequate water supply. Meanwhile, unstable stratification existed over Shandong Province. At lower levels, the warm and moist southwestern flow met with the cold northeastern flow. The warm air was uplifted by cold air, which released convective available potential energy and triggered convection. The special topography of the area also contributed to the increased rainfall.
The moist wave-activity density and wave-activity flux divergence in Eq. (36) were calculated with grid-analysis data. The data were produced by the Advanced Regional Prediction System (ARPS) Data Analysis System (ADAS) module of the ARPS model, forced by the National Centers for Environmental Prediction (NCEP) global real-time analysis data, surface observations and soundings. Owing to the limitation of the analysis data, the terms 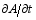
The observations of 6-h accumulated rainfall lay in the region 34-38°N at 1800 UTC 18 July 2007 (Fig. 1). In order to analyse the regional characteristics of wave- activity density, the zonal average was conducted in the calculation. The high-value area of wave-activity density was located in the middle-lower level troposphere over
the precipitation. Its center appeared near the ground layer. The positive high value was caused by the potential enstrophy perturbation term ( 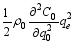
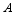
The precipitation area appeared as a band-like distribution between 1800 UTC 18 July 2007 and 1200 UTC 19 July 2007 (Fig. 2). At 1800 UTC 18 July 2007, the rain
band stretched northeastwards from the south of Shanxi Province to the southeast of Heilongjiang Province, with the two centers near (35°N, 117°E) and (36°N, 121°E). In order to investigate the overall characteristics of perturbation, the vertical integration was conducted for the whole troposphere. The vertically-integrated high-value area of wave-activity density showed a band-like pattern stretching northeastwards, and covered the rain band. After that, the rain band over the border of Henan and Shanxi provinces maintained, and the main body of the rain band over Shandong Province moved southwards. At 0600 UTC 19 July 2007, the rain band lay in the region (31-36°N, 108- 117°E), after which the main body of the rain band stretched eastwards and the rain cell in Jiangsu Province increased. The positive high-value belt of wave-activity density overlapped the rain band and moved southwards with the rain band in the period concerned. Therefore, the wave-activity density was consistent with the precipitation in terms of spatial distribution.
Figure 3 presents the temporal tendencies of wave- activity density and precipitation. The rain band appeared from 0600 UTC 18 July 2007 to 0000 UTC 21 July 2007. During the period of 0600 UTC 18 July 2007 to 1200 UTC 20 July 2007, the rain band moved southwards and then maintained until 0000 UTC 21 July 2007. The wave-activity density shared a belt-like pattern with the precipitation. The high-value belt of wave-activity density always covered the rain belt and moved southwards with the rain belt. The three centers near 40°N, 36°N, and 33°N corresponded to the three precipitation centers. Therefore, the wave-activity density was consistent with the rain belt in terms of temporal tendency.
To summarize, the wave-activity density shared a spatial pattern and temporal trend with the precipitation, and always covered it. This meant that the disturbance represented by the wave-activity density in the middle-lower level troposphere was closely related to the occurrence and development of precipitation.
To analyze the factors dominating the local change of wave-activity density, we calculated the wave-activity flux divergence and the additional two terms in Eq. (36). As shown in Fig. 4, in the period concerned, the three terms were abnormal in the rain belt. This indicated all of the three terms contributed to the wave-activity density. Comparing the three terms shows that the covariance of the solenoid and gradient of water vapor exerted the most marked influence, and the wave-activity flux divergence was the second-most important. The zonal gradient of difference between general potential temperature and potential temperature perturbations was the smallest in magnitude. Therefore, it contributed a little to the wave-activity density.
Existing theories of wave-flow interaction do not involve water vapor and are applicable to large-scale systems only. In the present paper we considered water vapor to derive the pseudomomentum wave-activity relation with the Momentum-Casimir method. Built in to the ageostrophic and non-hydrostatic dynamic framework, the wave-activity relation is applicable to mesoscale systems. Besides the wave-activity flux divergence and source or sink, the relation contains two additional forcing terms.
The wave-activity relation was applied to a precipitation event, and analysis revealed that the wave-activity density (its primary component being the potential enstrophy perturbation) maintained consistency with precipitation in terms of spatial distribution and temporal trend. This indicated that the perturbation represented by the wave-activity density in the middle-lower level troposphere was closely related to the occurrence and development of precipitation. The wave-activity flux divergence and the two additional forcing terms in the wave- activity relation contributed to the local change of wave- activity density. The covariance of the solenoid and gradient of water vapor made the primary contribution to the local change of wave-activity density, meaning that water vapor plays an important role in the development of perturbation. The wave-activity flux divergence was weaker than the covariance, but much stronger than the zonal gradient term.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|



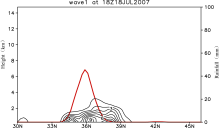
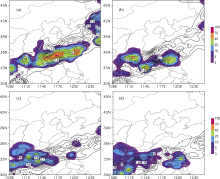
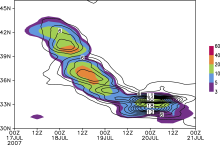
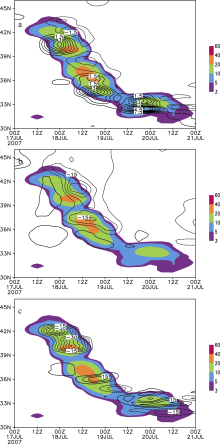
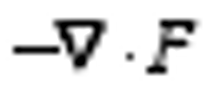 (units: 103 kg m-1 s-2); (b)
(units: 103 kg m-1 s-2); (b)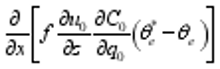 (units: 10-2 kg m-1 s-2); and (c)
(units: 10-2 kg m-1 s-2); and (c)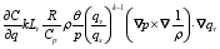 (units: 103 kg m-1 s-2) zonally- averaged over the longitude belt 117-121°E and vertically-integrated for the period 0000 UTC 17 July 2007 to 0000 UTC 21 July 2007. The shading denotes the observation of 6-h accumulated surface rainfall zonally-averaged over the longitude belt 117-121°E (units: mm).
(units: 103 kg m-1 s-2) zonally- averaged over the longitude belt 117-121°E and vertically-integrated for the period 0000 UTC 17 July 2007 to 0000 UTC 21 July 2007. The shading denotes the observation of 6-h accumulated surface rainfall zonally-averaged over the longitude belt 117-121°E (units: mm).